クラスや学年などで何十人かが集まると、同じ誕生日の人達がいる、ということが時折起こります。一方で、自分と同じ誕生日の人がいることは、ほとんどないような気がしませんか？
それは、自分と同じ誕生日の人が少ないからでしょうか？それとも別の理由があるのでしょうか？確率を使って、その理由を考えてみましょう。
この記事は、高校生以上を教える先生方に向けて、確率に関する問題をいくつか紹介しています。授業の導入などにお使いください。

同じ誕生日の人が２人いる確率は？

無作為に３０人を集めたとき、誕生日が同じである２人の組は少なくとも１組いるでしょうか？それともいないでしょうか？
１年を３６５日とすると、１月１日から１２月３１日まで、異なる誕生日は全部で３６５通りあるわけだから、３０人では感覚的に「いない」と考える人が多いのではないでしょうか。
ところがこの場合、誕生日が同じである２人の組は、７０％以上の確率でいることになります。
今回は、すべての日付の出生率が同じとして、このことを確率の計算を使って確認してみましょう。

３０人全員の誕生日が違う確率

まず、３０人全員の誕生日がそれぞれ違う確率を求めます。 はじめに、３０人の中から適当に１人の人を選びます。次に、もう１人の人を選ぶと、この人が１人目と違う誕生日である確率は\(\frac{364}{365}\)となります。つぎに３人目を選び、この人が１人目、２人目と違う誕生日である確率は\(\frac{363}{365}\)、さらに４人目が１、２、３人目と違う誕生日である確率は\(\frac{362}{365}\)となり、次々に続けていくと、最後の３０人目が１、２、……、２９人目と違う誕生日である確率は\(\frac{336}{365}\)となります。したがって、３０人全員が違う誕生日である確率は、

$$\frac{364}{365}\times\frac{363}{365}\times\frac{362}{365}\times … … \times\frac{336}{365}=0.29368 … …→約29\%$$

となります。
つまり、３０人がそれぞれバラバラの誕生日である確率は、約２９％であり、逆に７１％の確率で同じ誕生日の２人組が少なくとも１組はいることになるのです。

意外に高い確率で同じ誕生日の人がいるものだと思いませんか？

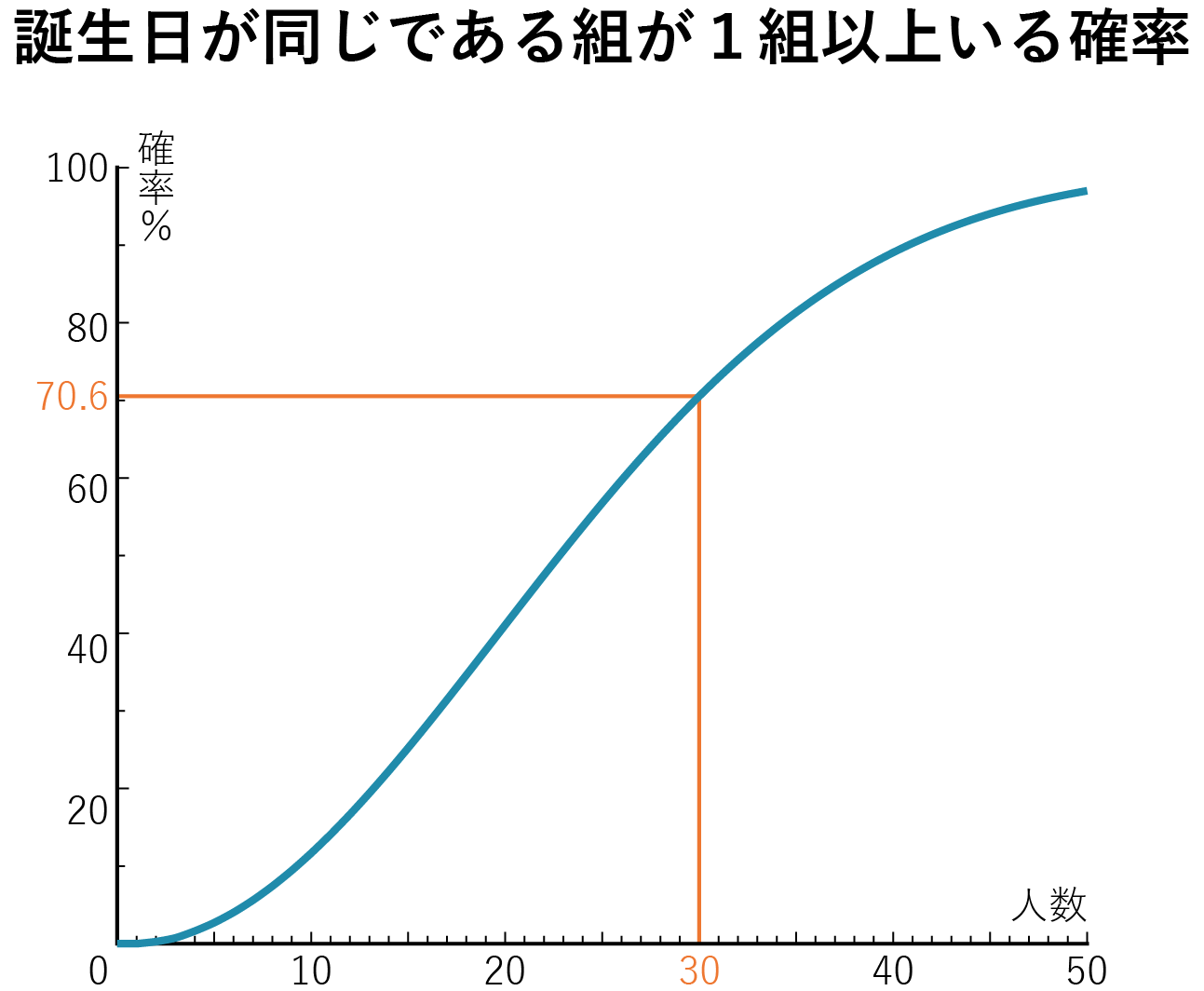
ちなみに、２３人集まれば約５０％の確率で同じ誕生日の２人組がいることになり、５０人集まれば約９７％の確率で同じ誕生日の２人組がいることになります。（グラフ参照）

あなたと同じ誕生日の人がいる確率は？

しかし、これは自分と同じ誕生日の人がいる確率とは違います。
あなたを含めた３０人の中に、あなたと同じ誕生日の人がいる確率は次のようになります。

あなた以外の２９人の中から１人目をつれてきます。この人があなたと違う誕生日である確率は、\(\frac{364}{365}\)です。２人目をつれてきて、この人もあなたと違う誕生日である確率は\(\frac{364}{365}\)です。同様に、２９人の１人１人について、あなたと違う誕生日である確率はそれぞれ\(\frac{364}{365}\)だから、２９人全員があなたと違う誕生日である確率は、

$$\frac{364}{365}\times\frac{364}{365}\times … … \times\frac{364}{365}$$

と\(\frac{364}{365}\)を２９回掛け合わせた値となり、この値は\(0.923 … …\)となります。 つまり、あなたと同じ誕生日の人がいる確率は８％以下ということになります。

もっと考えてみよう！

あなたの学校のクラスの中に、あなたと同じ誕生日の人が少なくとも１人いるおよその確率を計算してみましょう。

（ヒント：\(\frac{364}{365}=0.997\)として、電卓で計算しましょう。）