算数・数学の世界　「間接証明の種類」

ある命題が正しいこと（または誤っていること）を論理的に示す過程を「証明」といいます。数学では、様々な「証明」が出てきます。多くの「証明」では、正しいことが確認できている定義や仮定から出発して、「\(P\)である」と「\(P\)ならば\(Q\)」を組み合わせて「\(Q\)である」とし、また「\(Q\)ならば\(R\)」だから「\(R\)が成り立つ」という議論をくりかえして、結論にたどり着きます。このような証明を「直接証明」と呼びます。

しかし、なかには直接証明が困難な命題もあります。
そのような命題のなかには、間接証明と呼ばれるテクニックを用いることで、証明できることが知られている命題が、数多くあります。

この記事では、まず直接証明と間接証明の違いについて説明し、間接証明の代表的なものとして、対偶法、背理法、数学的帰納法を紹介します。

直接証明と間接証明

中学校の数学で習う証明の代表的なものは、図形分野における合同や相似の証明です。これらの証明は、「\(A\)ならば\(B\)、\(B\)ならば\(C\)、\(C\)ならば\(D\)、よって\(A\)ならば\(D\)である。」というように、いろいろな定義や定理を根拠にして論理を積み重ねていき、仮定から結論へストレートにたどり着く証明方法です。このような証明方法を「直接証明」といいます。これに対して、ある事柄が正しいことを、真偽が明確な他の事柄をもとに、間接的に示す証明方法を「間接証明」といいます。間接証明は、直接証明ではうまく説明できない事柄を示す際に用いられます。

数学の証明にはいろいろな種類がありますが、ここでは代表的な間接証明の手法をいくつか紹介します。

対偶法

対偶法は、証明する内容で、仮定と結論がはっきりしているときに用いられます。仮定よりも結論の方が簡単な場合に、対偶を利用することで簡単に証明ができます。

対偶とは

「\(P\)ならば\(Q\)」という命題があったとき、「\(Q\)でないならば\(P\)でない」を、もとの命題の対偶と呼びます。もとの命題が正しければ対偶も正しく、もとの命題が誤っているならば対偶も誤っている、という仕組みになっているため、対偶はとても重要です。

では、具体的な問題で考えてみましょう。

この中で論理的に正しいと言えるのは、BとCです。

ボールが入っているのは青い箱なので、B「開けた箱にボールが入っているならば、それは青い箱」は正しいと言えます。そして、この命題の対偶は、「開けた箱が青い箱でない（開けた箱が赤い箱）ならば、ボールは入っていない」で、つまりCと言えます。

また、何も入っていない青い箱も2箱あるので、A「開けた箱が青い箱ならば、ボールが入っている」は論理的には誤っています。そして、この命題の対偶は、「開けた箱にボールが入っていないならば、それは赤い箱」で、つまりDですが、箱に何も入っていなくても青い箱の可能性もあるので、これも誤りと言えます。

このように、もとの命題が正しければ対偶も正しく、もとの命題が誤っていれば対偶も誤っています。

真理集合

次に、\(n\)を\(10\)以下の自然数として、「\(n\)が\(4\)の倍数ならば、\(n\)は偶数」という命題について考えてみましょう。これを「\(P\)ならば\(Q\)」のかたちに当てはめると、\(P\)は「\(n\)が\(4\)の倍数」、\(Q\)は「\(n\)は偶数」ですね。具体的には、\(P\)は「\(4\)と\(8\)」、\(Q\)は「\(2\)，\(4\)，\(6\)，\(8\)，\(10\)」になります。これを図に表すと、下のようになります。

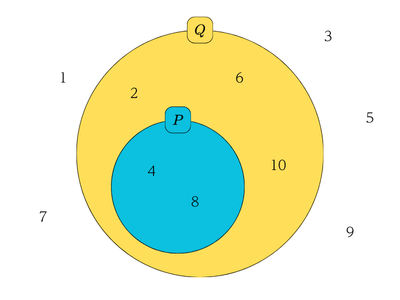
このように、命題の条件に合うものの集まりを、その命題の真理集合といい、このような図をベン図といいます。

このベン図を使って、「\(n\)が\(4\)の倍数ならば、\(n\)は偶数」が正しい理由を考えてみましょう。

\(P\)が\(Q\)に完全に含まれているので、\(n\)が\(P\)に含まれているとき、\(n\)は\(Q\)にも含まれていると言えます。このことから、\(n\)が\(P\)の条件を満たしていたら、\(Q\)の条件も満たす、つまり、\(P\)の真理集合が\(Q\)の真理集合に完全に含まれているとき、「\(P\)ならば\(Q\)」は正しいと言えます。

命題とその対偶の真偽が一致することの証明

では、同じようにベン図を使って、「\(n\)が\(4\)の倍数ならば、\(n\)は偶数」の対偶が正しいかどうかを見ていきましょう。

「\(P\)ならば\(Q\)」の対偶は、「\(Q\)でないならば\(P\)でない」でしたね。まず、“\(Q\)でない”は「\(n\)は偶数でない」、つまり「\(n\)は奇数」なので、「\(1\)，\(3\)，\(5\)，\(7\)，\(9\)」と言えます。“\(P\)でない”は「\(n\)が\(4\)の倍数でない」、つまり「\(1\)，\(2\)，\(3\)，\(5\)，\(6\)，\(7\)，\(9\)，\(10\)」です。

ベン図を使って考えると、“\(Q\)でない”の真理集合は\(Q\)の外側、“\(P\)でない”の真理集合は\(P\)の外側です。実際に図で表すと下のようになります。

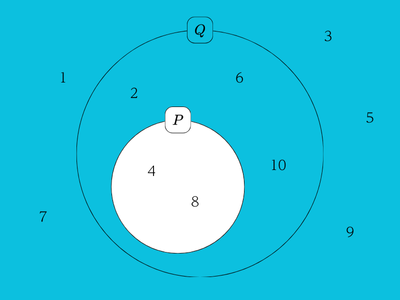
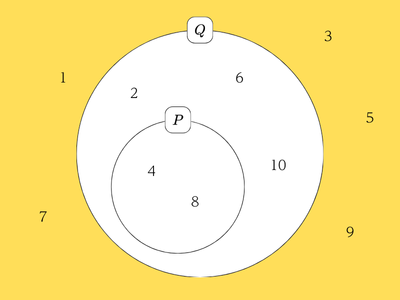
この図を見れば、\(Q\)でない「\(1\)，\(3\)，\(5\)，\(7\)，\(9\)」は、いずれも“\(P\)でない”の真理集合である\(P\)の外側に含まれていることがわかります。
この図から、「\(Q\)でない条件に合う範囲」が「\(P\)でない条件に合う範囲」に完全に含まれているので、「\(n\)が奇数ならば、\(n\)は\(4\)の倍数でない」、つまり「\(Q\)でないならば\(P\)でない」は正しいと言えます。

命題が誤っている場合も見てみましょう。

同じように\(n\)を\(10\)以下の自然数として、「\(n\)が\(3\)の倍数ならば、\(n\)は奇数」という命題を「\(P\)ならば\(Q\)」に当てはめると、\(P\)は「\(3\)，\(6\)，\(9\)」、\(Q\)は奇数なので、図で表すと下のようになります。

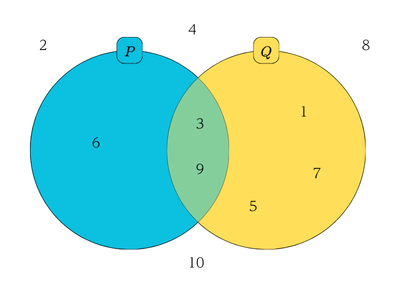
ベン図を見ると、\(P\)の真理集合のうち\(Q\)の真理集合に含まれていない部分がある（\(6\)が\(Q\)に含まれていない）ので、「\(n\)が\(3\)の倍数ならば、\(n\)は奇数」は正しくない（誤っている）と言えます。

対偶を考えると、ベン図は次のようになります。

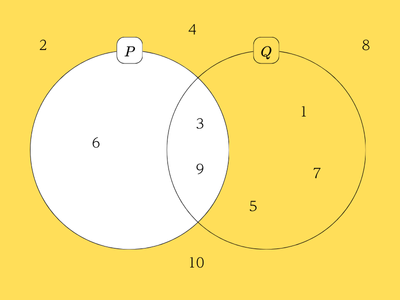
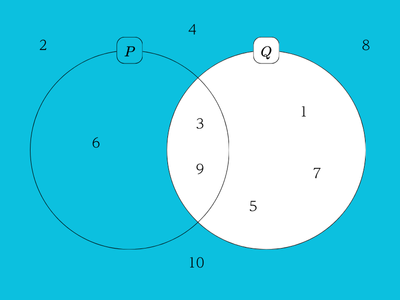
２つの図を見ると、\(6\)は\(Q\)でない範囲に入っていますが、\(P\)でない範囲には入っていないので、「\(n\)が奇数でないならば、\(n\)は\(3\)の倍数でない」は誤っていると言えます。

一般に、「\(P\)ならば\(Q\)」が正しいとき、もとの命題とその対偶のベン図は次のようになります。

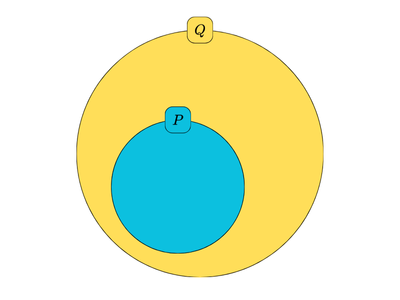
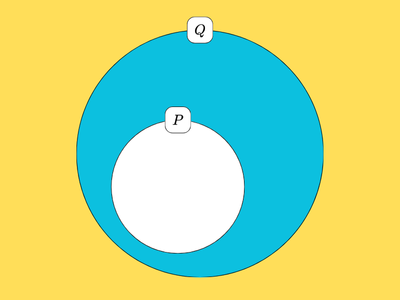
このベン図を見ると、もとの命題と対偶の真偽（正しいか誤っているか）は必ず一致することがわかります。
対偶法を使うと、次のような事柄を証明することができます。

対偶法の証明の例：\(n^2\)が\(3\)の倍数でないとき、\(n\)が\(6\)の倍数でないことの証明

この命題の対偶は、「\(n\)が\(6\)の倍数のとき、\(n^2\)が\(3\)の倍数」です。
この対偶が正しいことを証明すれば、\(n^2\)が\(3\)の倍数でないとき、\(n\)が\(6\)の倍数でないことが正しいことを証明できます。

\(n\) が\(6\)の倍数より、\(n=6k\) とおける（\(k\)は自然数）。
\(n^2=(6k)^2=36k^2=3×12k^2\)
\(k\)は自然数だから、\(12k^2\)も自然数なので、\(n^2=3×12k^2\) は\(3\)の倍数と言える。

よって、「\(n\)が\(6\)の倍数のとき、\(n^2\)が\(3\)の倍数」であることは、証明することができました。 したがって、もとの命題である「\(n^2\)が\(3\)の倍数でないとき、\(n\)が\(6\)の倍数でない」も、正しいことが証明できました。

背理法

背理法による証明は、「矛盾が生じたのは、\(P\)が成り立つとした初めの仮定が誤りであったためで、すなわち\(P\)は成り立たない」という論法です。
以下に、背理法による証明の例を紹介します。

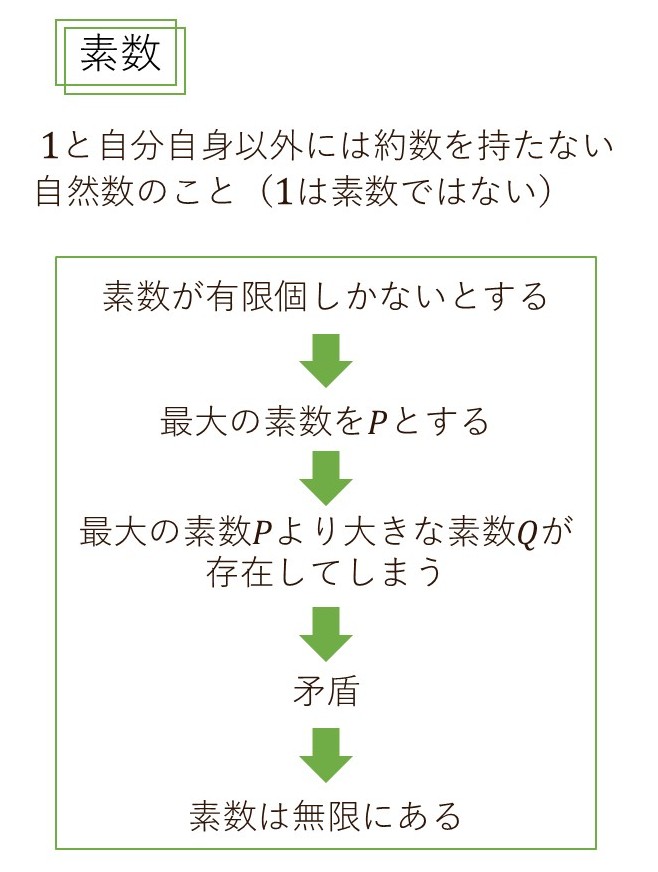
背理法の証明の例1：素数が無限にあることの証明

これは「素数の話」の記事でも紹介した証明方法です。

素数が有限個しかないと仮定する。
その場合、最大の素数が存在することになり、その数を\(P\)とする。

次に、\(2\)から\(P\)までのすべての素数の積に\(1\)を加えた数\(Q\)を考える。
\(Q=2×3×5×7×\space……\space×P＋1\)

このとき、
①　\(Q\)がもし素数であるとすると……
\(Q\)は\(P\)より大きい数なので、\(P\)が最大の素数であるということに矛盾。

よって、\(Q\)は素数ではいけないので、
②　\(Q\)がもし素数でないとすると……
\(Q\)は\(P\)以下のいずれかの素数で割り切れるはずだが、
\(Q\)の第1項（\(2×3×5×7×\space……\space×P\)）は\(2\)から\(P\)までのどの素数でも割り切れて、それに\(1\)を加えているので、\(Q\)は\(2\)から\(P\)までのどの素数で割っても余りが\(1\)となる。
よって、\(Q\)は\(2\)から\(P\)までのすべての素数で割り切れないので矛盾。

①、②のいずれにせよ矛盾。
これにより、「素数が有限個しかない」という最初の仮定をすると、必ず矛盾が生じるので、この仮定自体が誤りであったことがわかる。
よって、素数は無限にある。

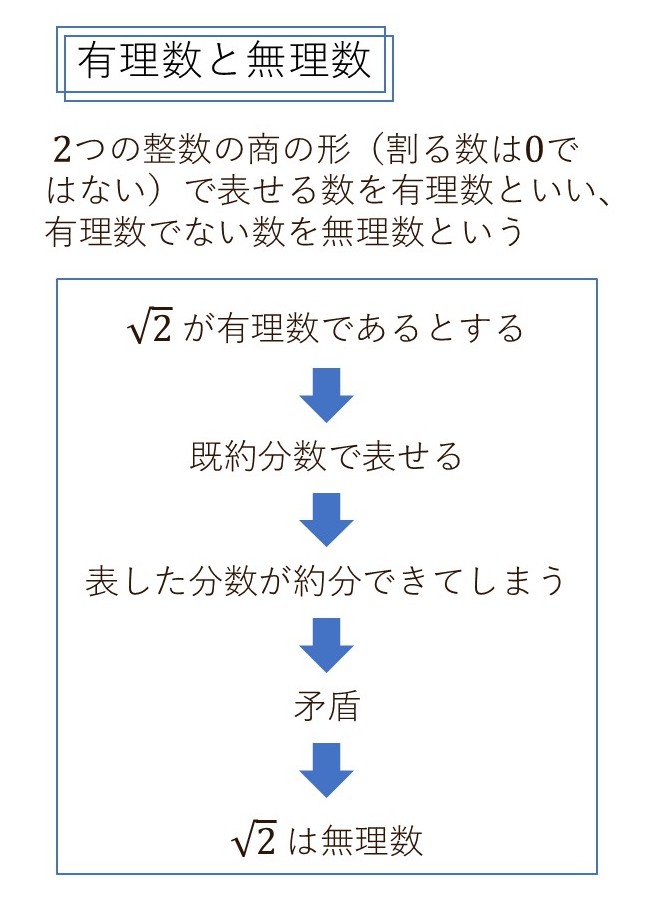
背理法の証明の例2：\(\sqrt{2}\) が無理数であることの証明

\(\sqrt{2}\)が有理数であると仮定する。
仮定より、

\(\displaystyle \sqrt{2}=\frac{n}{m}\) …①

とおける。
ただし、①の右辺は約分できるまで約分し、\(m\)，\(n\)は互いに素な（\(1\)以外に公約数をもたない）自然数とする。
★このような分数を既約分数という。

①の両辺を2乗すると、

\(2=(\frac{n}{m}) ^2\)
\(2m^2=n^2\) …②

②より、\(n\)は偶数（2乗して偶数になる自然数は偶数）。
よって、 \(n=2k\)とおける（\(k\)は自然数）。
②に代入すると、

\(2m^2=4k^2\)
\(m^2=2k^2\) …③

③より、\(m\)は偶数。

\(n\)も\(m\)も偶数であるということは、\(2\)で約分できるので、 \(n\)と\(m\)が互いに素であるという最初の仮定と矛盾する。
したがって、\(\sqrt{2}\)は無理数である。

背理法を使うときの注意

背理法はとても便利な証明方法なのですが、使い方を誤るとただの詭弁（こじつけ）になってしまうので、注意しましょう。次の背理法の使い方は、証明の結果自体は正しいのですが、証明の方法としては正しくありません。その理由を考えてみましょう。

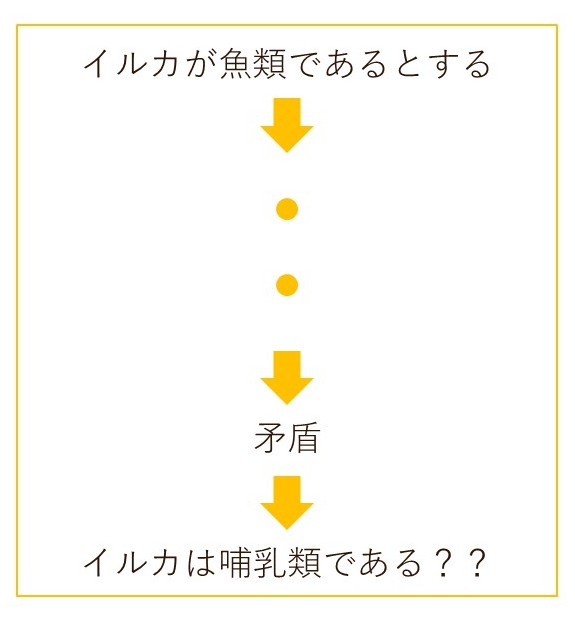
誤った背理法の使い方：イルカが哺乳類であることの証明

イルカは魚類であると仮定する…①
魚類はエラ呼吸する…②

①、②より、イルカはエラ呼吸するという結論が導けるが、実際イルカは肺呼吸をする動物である。
このことより、最初の仮定が誤りなので、イルカは哺乳類である。

例1、例2の正しい証明では、仮定した内容は証明したい内容のちょうど反対になっています。
反対になっているということは、例1の場合、「素数の個数が有限でないなら無限である」と言い切れる、例2の場合、「\(\sqrt{2}\)が有理数でないなら無理数である」と言い切れるということです。

これに対し、誤った例で仮定した「魚類である」という内容は、証明したいこと「哺乳類である」の反対にはなっていません。「魚類でないなら、哺乳類である」と言い切ることができないのです。このことから、これは誤った背理法の使い方であることがわかります。

数学的帰納法

数学的帰納法は、まず\(P\)に当てはまる最小の値の場合が証明され（A）、次に任意の文字で置き換えた際に\(P\)が成り立つと仮定し、置き換えた文字の次に大きな値の場合に成り立つことが証明されれば（B）、文字にどのような値を代入しても\(P\)は成り立つと考える論法です。
これは「フィボナッチ数列と黄金比」の記事でも紹介されています。

以下に、数学的帰納法による証明の例を紹介します。

数学的帰納法を使った証明の例：L字タイルの敷き詰め問題

命題
「\( 2^n\times2^n\)個の正方形のマス目がある。マス目のうち好きな1か所を黒く塗る。
すると、残りのマスを次のようなL字の図形で隙間なく敷き詰めることができる。」

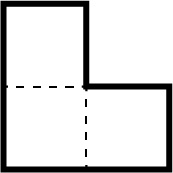
\(n=3\)のときの例

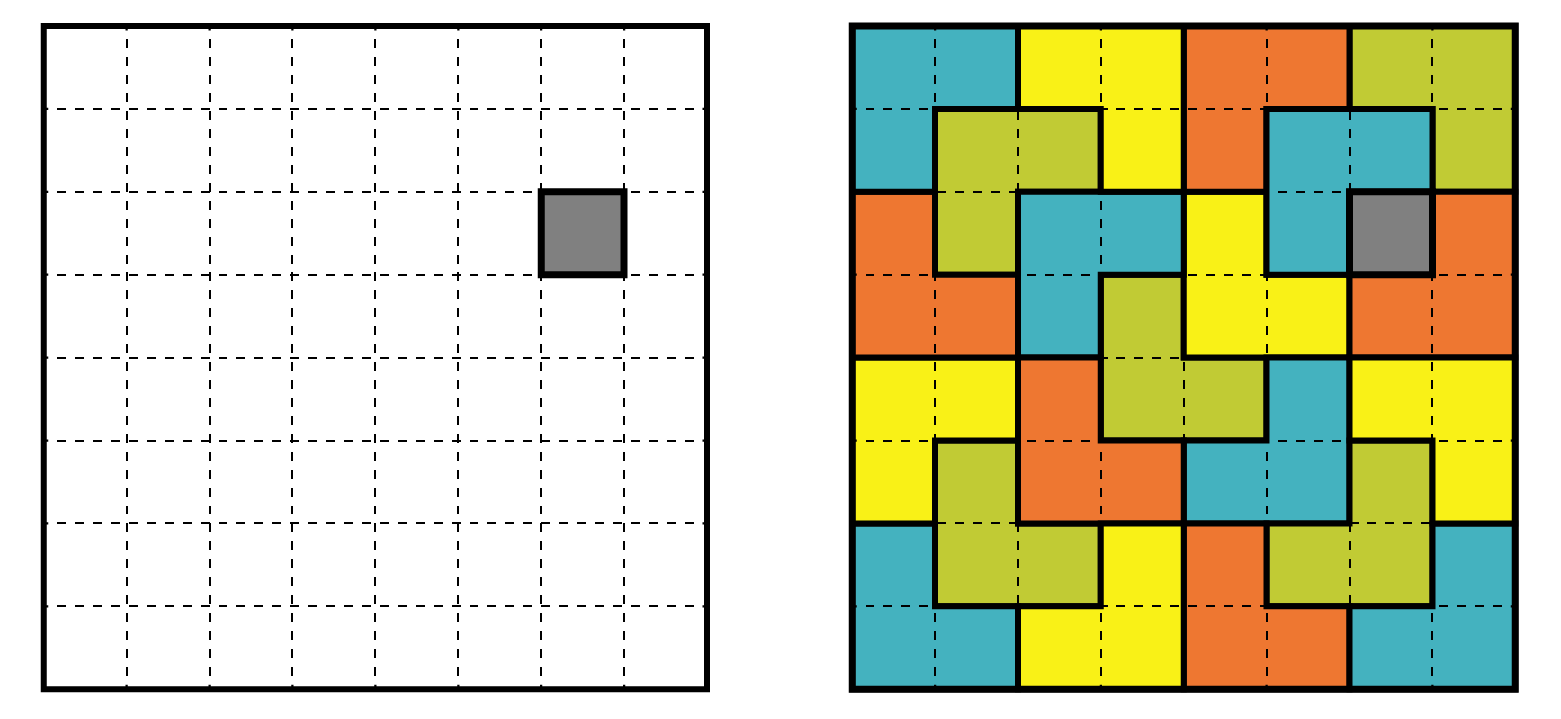
この命題を数学的帰納法を用いて示す。
A. \(n=1\)のとき、\(2 \times 2\)マスの中の\(1\)マスを黒く塗ると、残りはL字の図形と同じ形なので、敷き詰めることができる。

B. \(n=k\)のとき敷き詰めることができると仮定する。
\(n=k+1\)のとき、マス目は\(2^k\times2^k\)の正方形4つに分割できる。
このうち1つの正方形は、黒く塗られたマス目をもつ正方形だから、仮定より、L字の図形を敷き詰めることができる。
残りの3つの正方形は、分割前の正方形の中心に一番近いマスを灰色に塗ると、仮定から灰色に塗られていないマスにL字の図形を敷き詰めることができる。
最後に、分割した正方形を戻して、もとの\(2^{k+1}\times2^{k+1}\)マスの大きな正方形にして、中央の灰色のマスにL字の図形を置けば、\(n=k+1\)のときも敷き詰めることができる。

A. B.より、数学的帰納法を用いて、すべての自然数\(n\)に対して、\(2^n\times2^n\)個の正方形のマス目から任意の\(1\)マスを除いた残りのマス目にL字の図形を敷き詰めることができる。

数学的帰納法を使うときの注意

背理法と同じように、数学的帰納法も使い方を誤るとただの詭弁（こじつけ）になってしまうので、注意しましょう。次の証明の結論は明らかに間違っています。では、証明のどの部分が間違っているのでしょうか。

誤った数学的帰納法による証明：砂山のパラドックス

目の前に、砂山があるとします。この砂山から\(n\)粒の砂を取り除くことを考えます。

A. \(n\)を1として、砂山から砂をたった1粒を取り除いたとしても、砂山は砂山のままです。

B. 砂山から砂を\(k\)粒取り除いても、砂山は砂山のままであると仮定します。
すると、そこからさらに砂をたった1粒取り除いても、砂山は砂山のままと言えるので、はじめの砂山から合わせて\(k+1\)粒の砂を取り除いた時も砂山は砂山のままです。

A. B.より、砂山から何粒の砂を取り除いても砂山は砂山のままと言えます。よって、砂山から砂粒を全部取り去って、0粒になっても、それは砂山と言えます。

この数学的帰納法による証明では、砂山がどのようなものかをきちんと定めていないことが問題です。Bで、「砂山から1粒取り除いても砂山は砂山のままと言える」としていますが、本当にそうでしょうか。感覚としては正しいように思えるかもしれませんが、砂山から砂を取り去っていったら、どこかで砂山ではなくなるはずです。

どこで砂山から砂山でなくなるとするかは人によって違うかもしれないので、証明を始める前に、砂山がどのようなものかを明確に決めておく必要があります。例えば、「砂山であるためには砂粒が1億粒はなければならない」というように決めておけば、砂山から砂粒を1粒ずつ取っていくと、どこかで残りの砂粒が1億個未満となって、砂山とは言えなくなります。

練習問題

 \(\sqrt{ 2 }\)が無理数であることを利用して、\(\sqrt{ 2 }+3\)が無理数であることを証明しましょう。

解答

背理法を利用して証明する。
\(\sqrt{ 2 }+3\)が有理数であると仮定する。

\(\sqrt{ 2 }+3=\frac{n}{m}\) …①

とおける(\(n\), \(m\)は互いに素である自然数)。

①を変形すると、

\(\sqrt{ 2 }=\frac{n}{m}-3\) …②

②において、左辺は無理数、右辺は有理数となり矛盾している。
よって、最初の仮定が誤りであったことがわかり、\(\sqrt{ 2 }+3\)は無理数である。