算数・数学の世界「フィボナッチ数列と黄金比」

トップページ＞教育小ネタ帳＞算数・数学の世界「フィボナッチ数列と黄金比」

公開日：2024年06月14日　　
更新日：2024年06月14日

算数・数学の世界「フィボナッチ数列と黄金比」

授業導入算数・数学の世界高校生

フィボナッチ数列とは？
自然界に見出すフィボナッチ数列
フィボナッチ数列の数学的な性質
黄金比と図形
- 黄金長方形
- 黄金螺旋
黄金比と美術
フィボナッチ数列の中の黄金比
- 隣接三項間の漸化式
- フィボナッチ数列と黄金比の関係を表す証明
もっと考えてみよう！

フィボナッチ数列とよばれる数列を知っていますか？フィボナッチ数列は、自然界の様々なところに見出すことのできる身近な数列です。しかし、この数列を調べると、「人間が最も美しいと感じる」と言われている比、「黄金比」があらわれます。そして、フィボナッチ数列と黄金比の関係は、高校数学の知識を使って説明することができます。
この記事は、高校生を教える先生方に向けて、フィボナッチ数列と黄金比の関係にまつわる話を紹介しています。

フィボナッチ数列とは？

ある規則に従って数字を並べたものを、数列といいます。
例えば、最初の数字が1で、次の数字が前の数字より3ずつ大きくなるように数字を並べると、

$1, \ 4, \ 7, \ 10, \ 13, \ 16, \ 19, \ 22, \ 25, \ 28, \ 31, \ \cdots $

という数列ができます。

では、次の数列は、どのような規則にしたがって数が並んでいるでしょう。

$$\fbox{$0, \ 1, \ 1, \ 2, \ 3, \ 5, \ 8, \ 13, \ 21, \ 34, \ 55, \ 89, \ 144, \ 233, \ 377, \ 610, \ 987, \ 1597, \ 2584, \ 4181, \ \cdots\cdots$}$$

わかりましたか？
はじめの2つの数を除いたこの数列のそれぞれの数は、その1つ前の数と2つ前の数との和になっています。

$1=0+1, \ 2＝1+1, \ 3＝1+2, \ 5＝2+3, \ 8＝3+5, \ \cdots $

この数列はフィボナッチ数列と呼ばれています。「フィボナッチ」とは、12~13世紀のイタリアに実在した数学者の名前です。フィボナッチ数列に出現する数をフィボナッチ数といいます。
この数列がなぜ有名なのかというと、自然界の様々なところにこの数列を見出すことができるからなのです。

自然界に見出すフィボナッチ数列

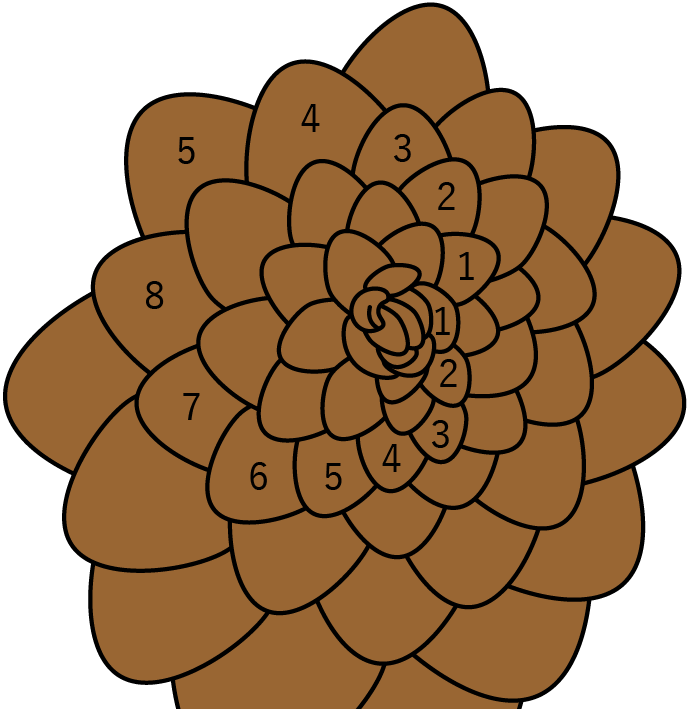
松ぼっくり

松ぼっくりのかさをよく観察してみると、右回りに8個ずつ、左回りに5個ずつ、または右回りに5個ずつ、左回りに3個ずつになっています。この$(8, \ 5)$、$(5, \ 3)$はフィボナッチ数です。

ひまわり

ひまわりの花をよく観察してみると、真ん中にある種は螺旋らせん状に並んでおり、種の並び方は
左回りに21列と右回りに34列
左回りに34列と右回りに55列
左回りに55列と右回りに89列
のいずれかになっていることが多くあります。これらの$(21, \ 34)$、$(34, \ 55)$、$(55, \ 89)$もフィボナッチ数です。

木の枝の伸び方

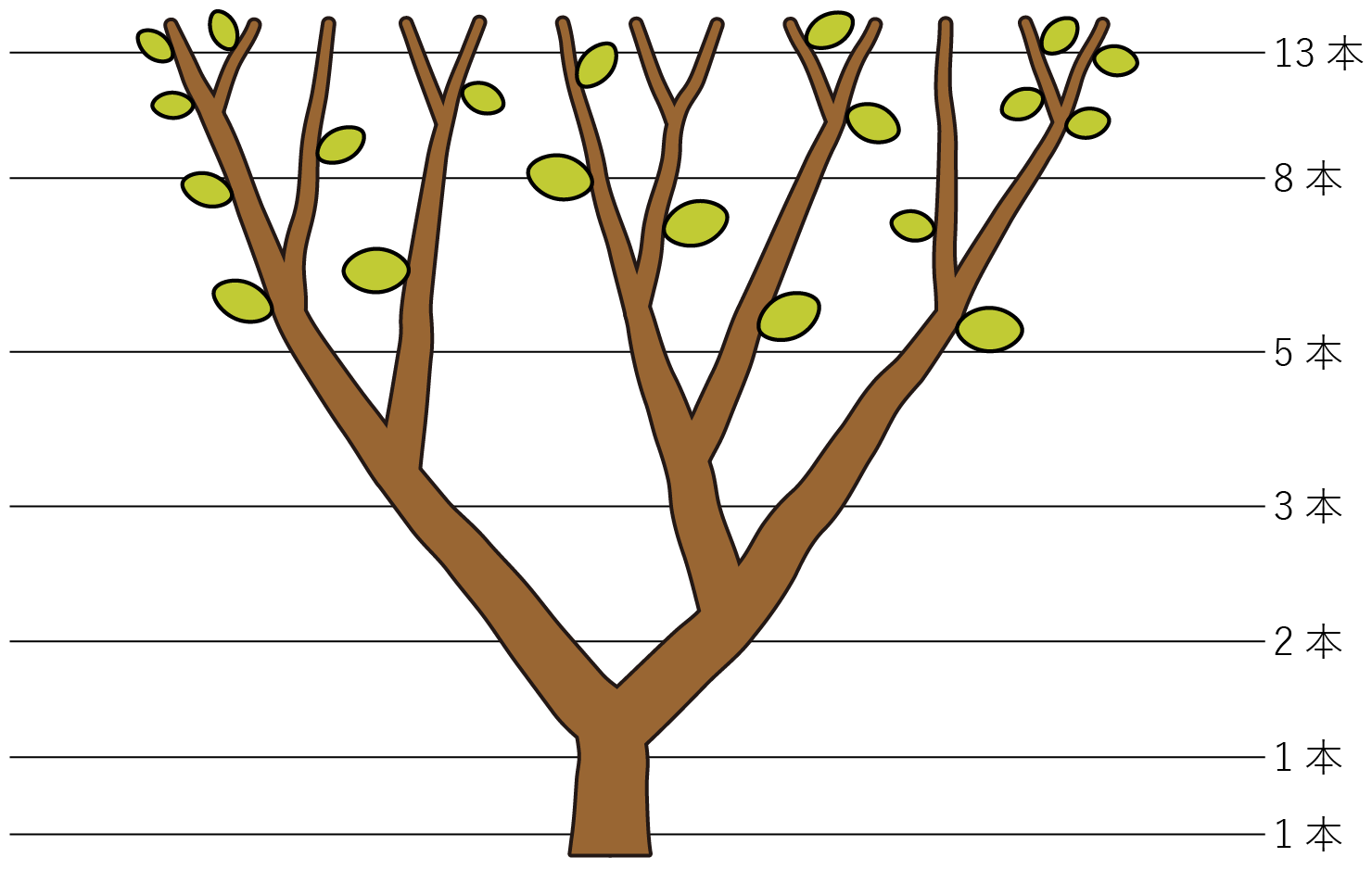
木の枝の伸び方もフィボナッチ数列で説明できます。
木の枝の伸び方は一般に次のルールで枝分かれすると考えられます。

ルール1: 枝は成長期に2本に分かれる。

ルール2: 枝が2本に分かれるとき、栄養は均等には配分されず、栄養の多い方、少ない方と偏りがある。栄養の多い方の枝は次の成長期に2本に分かれることができ、栄養の少ない方の枝は次の次の成長期に2本に分かれることができる。

この2つのルールに則って、枝分かれの様子を再現してみると次の図のようになります。各々の成長期における枝の本数は$1, \ 1, \ 2, \ 3, \ 5, \ 8, \ 13, \ \cdots $となり、フィボナッチ数列そのものです。

フィボナッチ数列の数学的な性質

このように、フィボナッチ数列は自然界に色々な形で顔を出しますが、数学的にも大変重要な数列で、興味深い性質がたくさんあります。

余りの周期数列

フィボナッチ数列の各項を2で割って、その余りを書き並べると、

$$ 0, \ 1, \ 1, \ 0, \ 1, \ 1, \ 0, \ 1, \ 1, \ 0, \ 1, \ 1, \ 0, \ 1, \ 1, \ \cdots $$

となり、 $(0, \ 1, \ 1)$ という周期が次々にくりかえす周期数列になります。これを「周期3」の周期数列といいます。

同様に各項を3で割ると、

$$ 0, \ 1, \ 1, \ 2, \ 0, \ 2, \ 2, \ 1, \ 0, \ 1, \ 1, \ 2, \ 0, \ 2, \ 2, \ 1, \ 0, \ 1, \ \cdots $$

となり、これは $(0, \ 1, \ 1, \ 2, \ 0, \ 2, \ 2, \ 1)$ という周期をくりかえすので、「周期8」。

各項を11で割ると、

$$ 0, \ 1, \ 1, \ 2, \ 3, \ 5, \ 8, \ 2, \ 10, \ 1, \ 0, \ 1, \ 1, \ 2, \ 3, \ 5, \ 8, \ 2, \ 10, \ 1, \ 0, \ \cdots $$

となり、これは $(0, \ 1, \ 1, \ 2, \ 3, \ 5, \ 8, \ 2, \ 10, \ 1)$ という周期をくりかえすので「周期10」の周期数列です。

一般に、
フィボナッチ数列の各項を2以上の整数で割ってその余りを並べてできる数列は、周期数列である
という性質が成り立ちます。

隣り合った二項は互いに素

また、
フィボナッチ数の隣り合う項は互いに素である
という性質もあります。

互いに素

2つの整数の共通の約数が1のみであるとき、これらの整数は「互いに素である」という。

このことを、背理法を使って以下に証明するので、興味のある方はご覧になってください。

背理法

あることがらPを示すのに、「Pが成り立つと仮定すると、矛盾が起こることを導く」ことにより、Pが成り立たないことを証明する手法。

フィボナッチ数列の$n$番目 $(n≧0)$ の項を$F_n$と表すことにすると、

$ F_0=0, \ F_1=1, \ F_{n+2}=F_n+F_{n+1} $

が成り立ちます。

ここで、隣り合ったフィボナッチ数$F_{n+2}$、$F_{n+1}$が互いに素ではない、つまり共通の約数$g$ $(g≧2)$を持つと仮定すると、自然数$a,\ b$を用いて$F_{n+2}=g\times a$、$F_{n+1}=g\times b$とおけます。
最初の式$F_{n+2}=F_n+F_{n+1}$より、$F_{n+2}-F_{n+1}=F_n$ということができます。
$g\times a-g\times b=F_n$、つまり$g\times\left(a-b\right)=F_n$となり、フィボナッチ数のすべての項は、$g$という$2$以上の約数を持つということになりますが、$F_1=1$、$F_2=1$であり、$g$という値は存在しません。このことより、最初の仮定が誤りであったと言うことができ、フィボナッチ数の隣り合う項は互いに素であると証明できます。

前の2つの数字を足していっているはずなのに
1以外の約数を持たないというのは不思議ですね！

2数の最大公約数

フィボナッチ数列の$n$番目 $(n≧0)$ の項を$F_n$と表すことにすると、

$ F_0=0, \ F_1=1, \ F_{n+2}=F_n+F_{n+1} $

が成り立ちます。

このとき、ある自然数$a, b$に対して、$a$と$b$の最大公約数を$c$とすると、フィボナッチ数$F_a$と$F_b$の最大公約数は、フィボナッチ数$F_c$になる
という定理があります。

例えば、$a=10$、$b=15$とすると、$a$と$b$の最大公約数は$5$になります。
ここで、$F_{10}=55$、$F_{15}=610$であり、その最大公約数は$5$で、$F_5$の値と同一です。

また、$a=14$、$b=21$とすると、$a$と$b$の最大公約数は$7$になります。
ここで、$F_{14}=377$、$F_{21}=10946$であり、その最大公約数は$13$で、$F_7$の値と同一です。

このことを、3つの定理を使って証明します。記号が多くて難しいですが、挑戦してみたい人はぜひご覧ください。

まずはフィボナッチ数列の加法定理を、数学的帰納法を使って証明します。

①フィボナッチ数列の加法定理

$a, \ b$は$1<a<b$を満たす自然数とする。
このとき次が成り立つ。

$F_b=F_a\times F_{b-a+1}+F_{a-1}\times F_{b-a} \cdots ① $

数学的帰納法

あることがらPを示すのに、
A. $n=1$ のとき、Pは成り立つ。
B. $n=k$ のとき、Pが成り立つと仮定すると、$n=k+1$ のときもPは成り立つ。
A、Bより、すべての自然数$n$に対してPは成り立つことを証明する手法。

<①-A>
$a=2$ のとき、$F_b=F_2\times F_{b-1}+F_1\times F_{b-2}$ となります。
ここで、$F_1=1$、$F_2=1$ なので、
$F_b=F_{b-1}+F_{b-2}$ となり、これはフィボナッチ数列の定義なので、正しいと言えます。

<①-B>
$a=k$（$k$は自然数）のとき、$F_b=F_k\times F_{b-k+1}+F_{k-1}\times F_{b-k}$ が成り立つと仮定します。
$a=k+1$（$k$は自然数）のとき、$F_b=F_{k+1}\times\ F_{b-(k+1)+1}+F_{(k+1)-1}\times\ F_{b-(k+1)}$ となり、
これを計算すると、

$ F_b=F_{k+1}\times\ F_{b-k}+F_k\times\ F_{b-k-1} $

フィボナッチ数列は $F_n=F_{n+2}-F_{n+1}$ と表されるので、$F_{b-k-1}$ は $F_{b-k-1}=$ $F_{b-k+1}-F_{b-k}$ と表せます。そのため、

$ F_b=F_{k+1}\times\ F_{b-k}+F_k\times($$F_{b-k+1}-F_{b-k}$$)$

$F_b=$$F_{k+1}\times F_{b-k}$$+$$F_k\times F_{b-k+1}$$-$$F_k\times F_{b-k}$

今、$F_b=$$F_k\times F_{b-k+1}$$+F_{k-1}\times\ F_{b-k}$ が成り立つと仮定しているので、これを利用して $F_k\times F_{b-k+1}$ の部分を $F_b-$$F_{k-1}\times F_{b-k}$ とすると、

$F_b=$$F_{k+1}\times F_{b-k}$$+(F_b-$$F_{k-1}\times F_{b-k}$$)-$$F_k\times F_{b-k}$

$F_{b-k}$ でくくると、

$F_b=F_b+F_{b-k}\times ($$F_{k+1}$$-$$F_k$$-$$F_{k-1}$$)$

かっこの中は、フィボナッチ数列の定義 $F_{n+2}-F_{n+1}-F_n=0$ より、$0$であるとわかります。
つまり、$F_b=F_b$ となり、$a=k+1$（$k$は自然数）のときも成り立つことがわかりました。
<①-A>、<①-B>より、すべての自然数に対して、

$ F_b=F_a\times F_{b-a+1}+F_{a-1}\times F_{b-a} $

が成り立つことがわかりました。

また、$F_b=F_a\times F_{b-a+1}+F_{a-1}\times F_{b-a}$の$b$の部分に$a+b$を当てはめると、

$ F_{a+b}=F_a\times F_{b+1}+F_{a-1}\times F_{b} \cdots ①’$

という式も成り立つことがわかります。

②最大公約数の定理(1)

$a,\ b$は自然数とする。
$a$と$b$が互いに素であるとき、$a$と$bc$（$c$は自然数）の最大公約数は、$a$と$c$の最大公約数に等しい。

③最大公約数の定理(2)

$a,\ b$は $1<a<b$ を満たす自然数とする。
このとき、$a$と$ab+r$の最大公約数は、$a$と$r$の最大公約数に等しい。

ここで、$a$、$ab+r$の共通の約数を$d$とおくと、
$a=dk$、$ab+r=dj$（$k,\ j$は自然数）と表すことができます。
ここで$r$は、$r=dj-dk\times\ b=d\left(j-bk\right)$となり、$r$もまた共通の約数$d$を持つことがわかります。
ここで、$d$は$a$と$ab+r$の共通の約数の総称なので、その最大公約数もまた$d$で表されます。
このことから、$a$と$ab+r$の最大公約数は、$a$と$r$の最大公約数に等しいことが証明できます。

フィボナッチ数列の最大公約数に関する証明

ある自然数$a,\ b$に対して、$a$と$b$の最大公約数を$c$とすると、フィボナッチ数$F_a$と$F_b$の最大公約数は、フィボナッチ数$F_c$になる
という定理を証明するために、まずは次の事柄を証明します。

$a,\ b$は$ 1<a<b$を満たす自然数とする。
$b=aq+r$ （$q, \ r$は自然数）、$0<r<a$であるとき、フィボナッチ数列の$a$番目の項を$F_a$、$b$番目の項を$F_b$と表すと、最大公約数 $gcd(F_a, \ F_b)$ は、$F_a$と$F_r$の最大公約数 $gcd(F_a, \ F_r)$ に等しい。

$gcd$ は英語で最大公約数を表す $greatest\ common\ divisor$ の略です！
例えば $gcd(18,\ 24)=6$ のように表されます。

ここでは$q$に関して、数学的帰納法を利用して証明します。

A.
$q=1$ のとき、$b=a+r$

$gcd($$F_a$$, \ $$F_b$$)$

$=gcd($$F_a$$, \ $$F_{a+r}$$)$

ここで①’を利用して$F_{a+r}$を変形します。

$=gcd($$F_a$$, \ $$F_a$$\times F_{r+1}+F_{a-1}\times $$F_r$$)$

③の定理より、

$=gcd($$F_a$$, \ F_{a-1}\times$$F_r$$)$

$F_a$と$F_{a-1}$は隣り合った二項である。これらは互いに素であるので、②の定理より、

$=gcd($$F_a$$, \ $$F_r$$)$

B.
$q=k$（$k$は自然数）のとき、$b=ak+r$

$gcd($$F_a$$, \ $$F_b$$)\ =gcd($$F_a$$,\ $$F_{ak+r}$$)=gcd($$F_a$$, \ $$F_r$$)$

が成り立つと仮定する。

$q=k+1$（$k$は自然数）のとき、
$b=a(k+1)+r$より、

$gcd($$F_a$$, \ $$F_b$$)$

$=gcd($$F_a$$, \ $$F_{a(k+1)+r}$$)$

$=gcd($$F_a$$, \ $$F_{a+ak+r}$$)$

①の定理より、

$=gcd($$F_a$$,\ $$F_a$$\times\ F_{ak+r+1}+F_{a-1}\times\ $$F_{ak+r}$$)$

③の定理より、

$=gcd($$F_a$$,\ F_{a-1}\times\ $$F_{ak+r}$$)$

$F_a$と$F_{a-1}$は互いに素であるので、②の定理より、

$=gcd($$F_a$$,\ $$F_{ak+r}$$)$

今、$gcd($$F_a$$, \ $$F_{ak+r}$$)=gcd($$F_a$$, \ $$F_r$$)$が成り立つと仮定しているので、これを利用して、

$=gcd($$F_a$$, \ $$F_r$$)$

A、Bよりすべての自然数に対して、

$gcd($$F_a$$, \ $$F_b$$)\ =gcd($$F_a$$, \ $$F_r$$)$

が成り立つことがわかりました。
ここで、ユークリッドの互除法の考え方を参照します。

ユークリッドの互除法

$a,\ b$は $1<a<b$ を満たす自然数とする。
$b=aq+r$ （$q, \ r$は自然数）なら、$a$と$b$の最大公約数$gcd(a, \ b)$は、$a$と$r$の最大公約数$gcd(a, \ r)$に等しい。

ユークリッドの互除法と、今証明した式を並べて、比べてみましょう。

$gcd($$a$$, \ $$b$$)=gcd($$a$$, \ $$r$$)$

$($$F_a$$, \ $$F_b$$)=gcd($$F_a$$, \ $$F_r$$)$

どちらの式でも、左辺の$a$$, \ $$b$が右辺では$a$$, \ $$r$に代わっています。

ところで、ユークリッドの互除法は、割り算のあまりを利用して、最大公約数を求める方法でした。割り算を繰り返して、あまり$r$の値が$0$になるとき、そのひとつ前のあまりが、もとの二つの数の最大公約数である、という定理です。

なので、互除法を続けていくと、

$gcd($$a$$,$$b$$)=gcd($$a$$,$$r$$)=$$\cdots\cdots=gcd(c,\ ck)=c（kは自然数）$

のようになって、最大公約数$c$を求めることができます。

フィボナッチ数列の一般項でも、同じように計算を続けていくと、

$gcd($$F_a$$, \ $$F_b$$)=gcd($$F_a$$, \ $$F_r$$)=$$\cdots\cdots=gcd(F_c,\ F_{ck})$

となります。
このとき、$gcd(F_c, \ F_{ck})=F_c$となるでしょうか。

そこで、次の事柄を証明します。

$c,\ k$ を自然数とする。フィボナッチ数列の$c$番目の項を$F_c$、$ck$番目の項を$F_{ck}$と表すと、次が成り立つ。

$gcd(F_c, \ F_{ck})=F_c$

$k$に関して、数学的帰納法を利用して証明します。

A.
$k=1$のとき、

$gcd(F_c,F_{ck})=gcd(F_c,\ F_c)=F_c$

B.
$k=j$（$j$は自然数）のとき、

$gcd(F_c, \ F_{cj})=F_c$

が成り立つと仮定する。
$k=j+1$のとき、

$gcd(F_c,\ F_{ck})=gcd(F_c,\ F_{c(j+1)})$

①の定理より、

$=gcd(F_c,\ F_c\times F_{cj+1}+F_{c-1}\times F_{cj})$

③の定理より、

$=gcd(F_c,\ F_{c-1}\times F_{cj})$

$F_c$と$F_{c-1}$は互いに素であるので、②の定理より、

$=gcd(F_c,\ F_{cj})=F_c$

A、Bよりすべての自然数に対して、

$gcd(F_c, \ F_{ck})=F_c$

が成り立つことがわかりました。

実際の数字を当てはめて考えてみましょう。

$a=208$、$b=169$のとき、ユークリッドの互除法を使って、

$208$$ \ \div \ $$169$$\ =1 \ あまり$$39$

$169$$ \ \div \ $$39$$\ =4 \ あまり$$13$

$39$$ \ \div \ $$13$$\ =3$

$gcd($$208$$, \ $$169$$) \ =gcd($$169$$, \ $$39$$) \ =gcd($$39$$, \ $$13$$) \ =$$13$

であり、$208$と$169$の最大公約数は$13$です。

先に証明した、$gcd($$F_a$$, \ $$F_b$$)\ =gcd($$F_a$$, \ $$F_r$$)$に$a=208$、$b=169$を当てはめると、

$gcd($$F_{208}$$, \ $$F_{169}$$) \ =gcd($$F_{169}$$, \ $$F_{39}$$) \ =gcd($$F_{39}$$, \ $$F_{13}$$) \ =$$F_{13}$

となることがわかります。

このことから、ある自然数$a, \ b$に対して、$a$と$b$の最大公約数を$c$とすると、フィボナッチ数$F_a$と$F_b$の最大公約数は、フィボナッチ数$F_c$になるということがわかりました。

黄金比と図形

黄金比とは、「人間が最も美しいと感じる」と言われている比率です。数式では$1:\frac{1+\sqrt 5}{2}$と表され、近似値では「$1:1.618$」、「$5:8$」という比率が使われます。
黄金比は私たちの身の回りの様々なところに使われています。例えば、名刺やクレジットカードなどのカード類の短辺と長辺の比は、黄金比に近い比が使われています。新書本や漫画の単行本のサイズにも、黄金比に近い比が使われているものがあります。また、会社のロゴに黄金比を取り入れている企業もあります。

黄金長方形

黄金長方形とは、縦横の長さの比が黄金比、すなわち$1:\frac{1+\sqrt 5}{2}$の長方形のことです。
一辺の長さがフィボナッチ数の正方形をつなぎ合わせてできる長方形の形は、黄金長方形に収束するという性質があります。

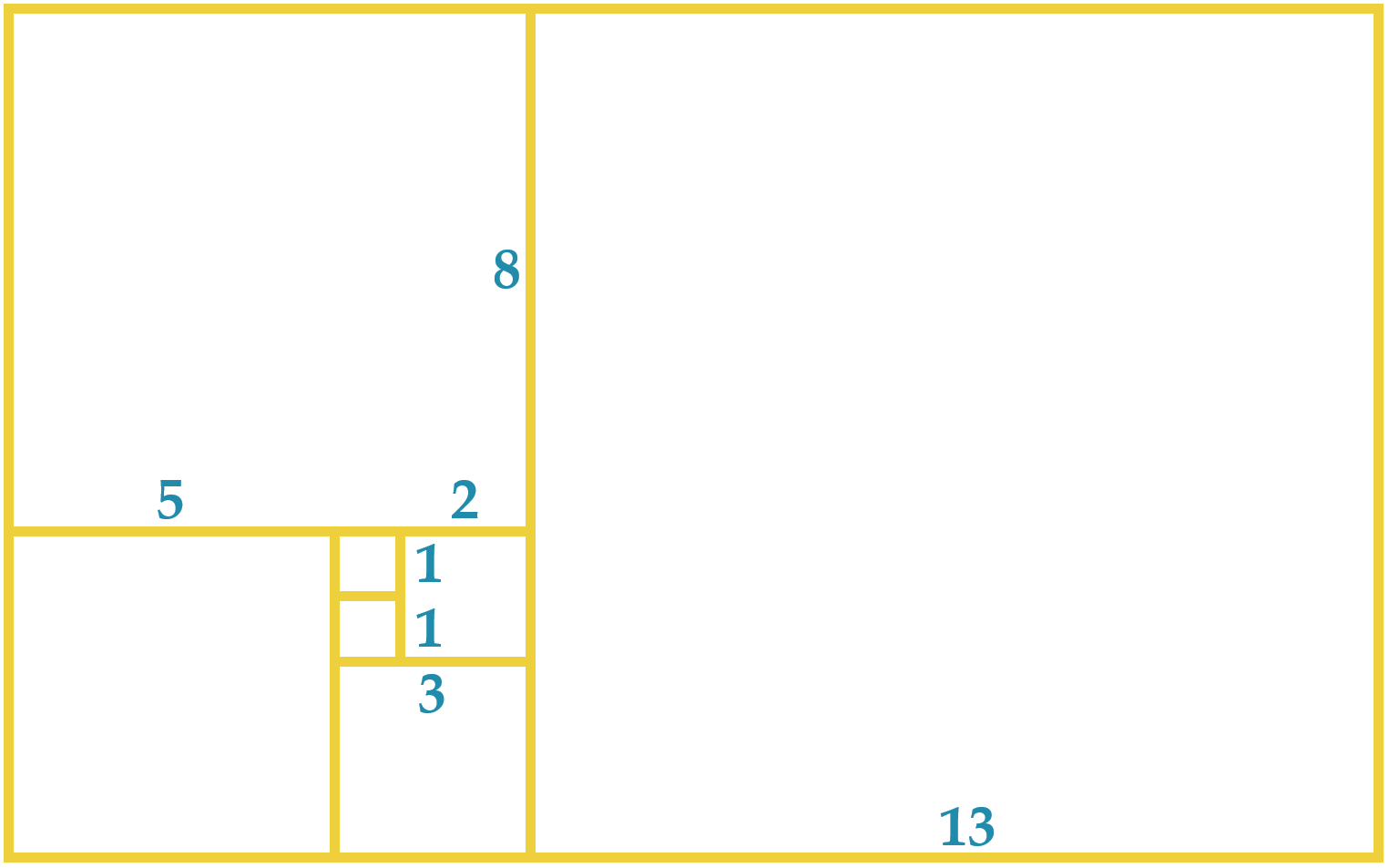
黄金螺旋

次の図のように、黄金長方形の内部にあるすべての正方形の、対角になっている点をなめらかにつなぐことで描かれる螺旋らせんを「黄金螺旋」と言います。

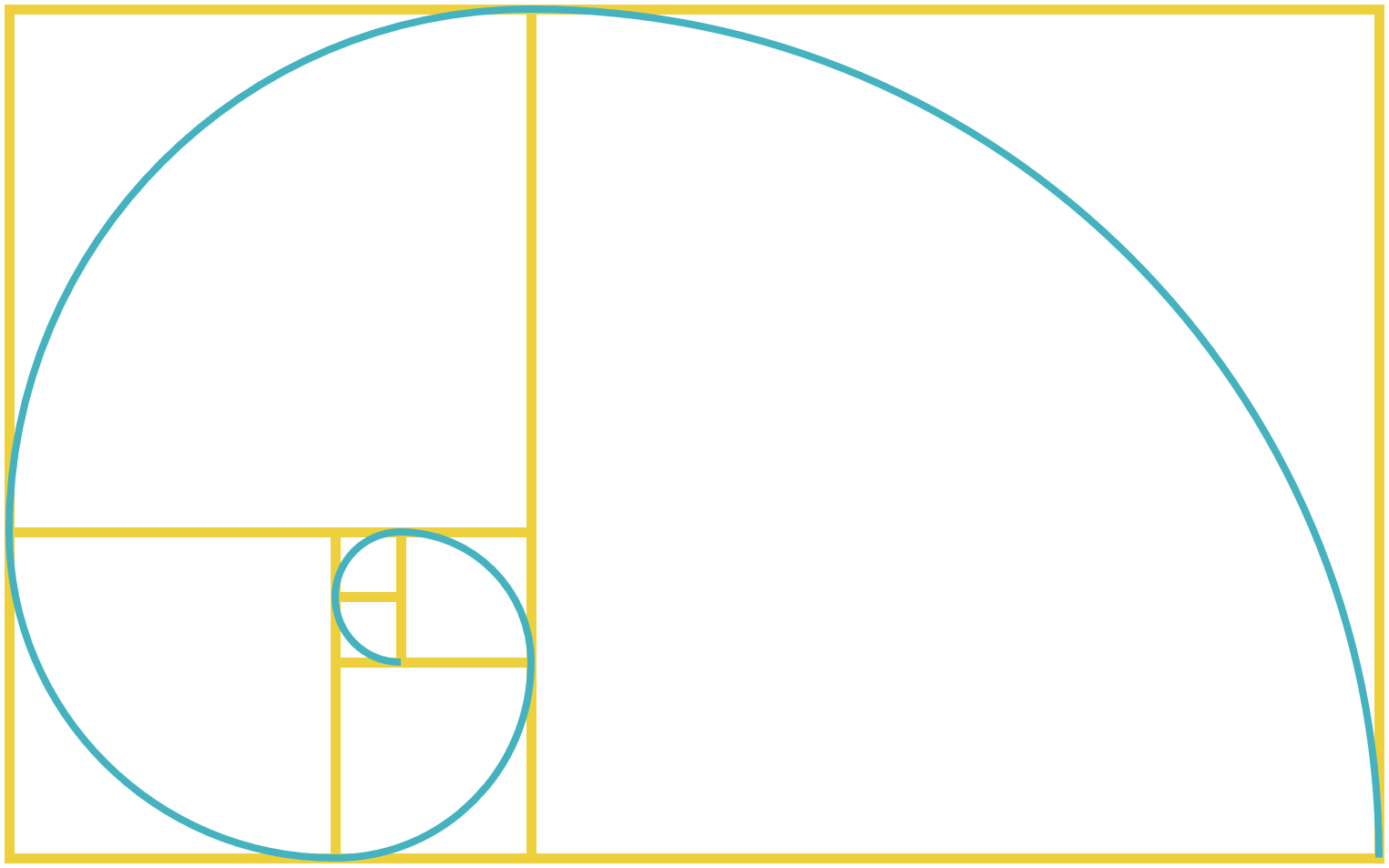
この黄金螺旋を目にしたことがある方も多いのではないでしょうか。前述したひまわりの種の並び方の他にも、オウムガイの殻やバラの花びらの重なり、DNAの螺旋構造などは、いずれも黄金螺旋に近しいといわれています。

黄金比と美術

黄金比は古来より人類が最も美しいと感じる比率とされ、時代や国境を越えて使われてきました。それは、世界的に有名な建築物や芸術作品に、意識的に、あるいは無意識的に、作家たちに応用されてきました。

モナ・リザ（イタリア）

レオナルド・ダ・ヴィンチが描いたモナ・リザは、顔の輪郭と上半身のバランスが黄金比になっています。

ピラミッド（エジプト）

ピラミッドの側面の三角形の高さと底辺の半分の長さの比は黄金比です。

パルテノン神殿（古代ギリシア）

この神殿を正面から見ると、縦、横の比はほぼ黄金比です。

ミロのヴィーナス（古代ギリシア）

この彫像は、身体の様々な部分に黄金比が応用されています。例えば、ヴィーナスの頭のてっぺんからおへそまでの長さと、おへそからつま先までの長さの比は黄金比になっています。

フィボナッチ数列の中の黄金比

ここで、もう一度フィボナッチ数列を見てみましょう。

$$ 0，1，1，2，3，5，8，13，21，34，55，89，144，233，\ \cdots $$

この数列の$0$を除いた隣り合う$2$数の比を、分数の形に並べて新しい数列を作ります。

$$\frac{1}{1}, \frac{2}{1}, \fbox{$\frac{3}{2}, \frac{5}{3}, \frac{8}{5}, \frac{13}{8}, \frac{21}{13}, \frac{34}{21}, \frac{55}{34}, \frac{89}{55}, \frac{144}{89}, \frac{233}{144}, \ \cdots\cdots$}$$

数学では、一見なんの関係もない2つのことがらが、実は密接に結ばれていたということがよくあります。
この罫線で囲まれた数列には終わりがありません。そして、この数列は決して到達できないある値に向かって永久に進んでいきます。その値こそ…

フィボナッチ数列の隣り合う2つの数の比は、黄金比に限りなく近づいていく

この数列の値は、項が進むにつれて黄金比に限りなく近づいていきます。このことを、「この数列は黄金比に収束する」といいます。
この数列が黄金比に収束することは、高校数学の知識で証明できます。

隣接三項間の漸化式

フィボナッチ数列の$n$番目 $(n≧0)$ の項を$F_n$と表すことにすると、

$F_0=0, \ F_1=1, \ F_{n+2}=F_n+F_{n+1}$

が成り立ちます。$F_{n+2}=F_n+F_{n+1}$はフィボナッチ数列の漸化式です。
漸化式とは「数列の中のある項を、それ以前の項を使いながら説明する式」のことで、フィボナッチ数列の漸化式$F_{n+2}=F_n+F_{n+1}$は「ある項は、その$1$つ前と$2$つ前の項の数を足し合わせたものである」ことを表します。
これは項数が$3$つある「三項間漸化式」と呼ばれるものです。この漸化式は、「特性方程式」という公式を使用して解くことができます。

特性方程式

隣接三項間の漸化式

$a_{n+2}+{pa}_{n+1}＋qa_n＝ 0$

の特性方程式$x^2+px+q=0$の$2$解が$\alpha, \ \beta$ ($\alpha≦\beta$) のとき、

\begin{equation*}
\begin{cases}
a_{n+2}- \alpha a_{n+1}= \beta (a_{n+1}- \alpha a_n)\\
a_{n+2}- \beta a_{n+1}= \alpha (a_{n+1}- \beta a_n)
\end{cases}
\end{equation*}

と変形できる。

これは最初の漸化式$a_{n+2}+{pa}_{n+1}＋qa_n＝ 0$の一般項$a_n$を、等比数列を利用して求める方法です。
一般項$a_n$とは、ある数列の第$n$項を、$n$の式で表したものです。例えば数列$\left\{1,3,5,7,9, \cdots\cdots\right\}$の一般項は$2n-1$と表すことができます。
等比数列とは、隣り合う$2$つの項の比が常に一定の数列のことで、$a_{n+1}=a_nr$と表すことができます。ここで$r$はかける数、公比を表します。
等比数列の一般項$a_n$は、$a_n=a_1\times\ r^{n-1}$、つまり（初項）×（公比）$^{n-1}$で表されます。

特性方程式の解説

ここで、フィボナッチ数列と黄金比の関係を表すために利用する、特性方程式について解説します。この内容は高校の数学Bで学習する内容なので、ご存じの方は読み飛ばしていただいても構いません。

まず例として、

$a_1＝ 0, \ a_2＝ 1, \ a_{n+2}-3a_{n+1}-10a_n＝ 0 \cdotsⅠ$

という数列の一般項を求めてみましょう。

ここで、真ん中の$-3a_{n+1}$を、$2a_{n+1}$と$-5a_{n+1}$という$2$つの数に分けて、$Ⅰ$を次のように変形します。

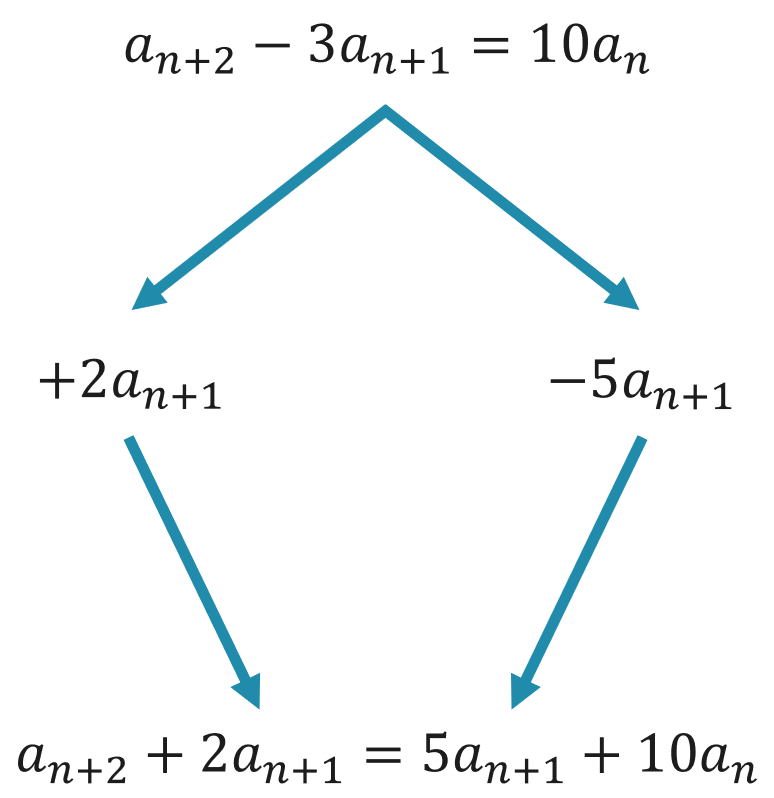
$$a_{n+2}+2a_{n+1}＝ 5(a_{n+1}+2a_n) \cdots ★$$

という形に変形できます。

同様に、$-5a_{n+1}$を左辺に残し、$+2a_{n+1}$を右辺に移項すると、

$$a_{n+2}-5a_{n+1}=-2(a_{n+1}-5a_n) \cdots ☆$$

という形に変形できます。

ここまでの内容を、文字$\alpha$と$\beta$ ($\alpha ≦ \beta$) を使用して一般化します。

\begin{equation*}
\begin{cases}
a_{n+2}-\alpha a_{n+1}= \beta (a_{n+1}- \alpha a_n) \cdots Ⅱ-①\\
a_{n+2}-\beta a_{n+1}= \alpha (a_{n+1}- \beta a_n) \cdots Ⅱ-②
\end{cases}
\end{equation*}

という式ができあがります。上の例だと、$\alpha=-2$、$\beta=5$ですね。
$Ⅱ$の2つの式はどちらも全く同じ意味を表していますが、後で一般項を求める際に、連立方程式として使用するので、意図的に2つの式に変形しています。

では、$Ⅱ−①$の式を展開してみると、

$a_{n+2}-\alpha\ a_{n+1}=\beta a_{n+1}-\alpha\beta a_n$

全ての項を左辺に集めて、

$a_{n+2}-\alpha\ a_{n+1}-\beta a_{n+1}+\alpha\beta a_n=0$

$a_{n+2}-(\alpha+\beta)a_{n+1}+\alpha\beta a_n=0$

という式ができあがります。

ここで、$Ⅰ$の式、$\ a_{n+2}-3a_{n+1}-10a_n＝ 0$と見比べると、

\begin{equation*}
\begin{cases}
\alpha + \beta =3\\
\alpha \beta =-10
\end{cases}
\end{equation*}

となる$\alpha$と$\beta$の組み合わせを見つければ、$Ⅱ$の式の形へ変形できそうです。上の例の$\alpha=-2$、$\beta=5$は、この組み合わせに当てはまっています。しかし、毎回あてずっぽうで組み合わせを考えるのは、かなり骨の折れる作業です。
そこで、「2次方程式の解と係数の関係」を思い出してみましょう。

2次方程式の解と係数の関係

2次方程式$ax^2+bx+c=0$の2つの解を$\alpha$, $\beta$とすると、

$\alpha+\beta=-\frac{b}{a},\ \ \alpha\beta=\frac{c}{a}$

が成り立つ。

今回は、$-\frac{b}{a}=3$、$\frac{c}{a}=-10$となります。
$ax^2+bx+c=0$に$a=1$、$b=-3$、$c=-10$を代入すると、$x^2-3x-10=0$となり、
$Ⅰ$の式、$a_{n+2}-3a_{n+1}-10a_n＝0$を$Ⅱ−①$の式、$a_{n+2}-\alpha a_{n+1}=\beta(a_{n+1}-\alpha a_n)$の形に変形するときの$\alpha$と$\beta$の値は、$x^2-3x-10=0$の解と同一であることがわかります。
二次方程式$x^2-3x-10=0$を解くと、因数分解して$(x+2)(x-5)=0$
$x=-2,\ 5$、つまり、$(\alpha,\ \beta)=(-2,\ 5)$ $(\alpha≦\beta)$
これを$Ⅱ$の式に当てはめると、

$a_{n+2}+2a_{n+1}=5($$\underline{a_{n+1}+2a_n}$$) \cdots Ⅲ$

$a_{n+2}-5a_{n+1}=-2($$\underline{a_{n+1}-5a_n}$$) \cdots Ⅳ$

これらの式はどこかで見たことがある……
あっ！前に出てきた★☆のペアですね！

ここで、$Ⅲ$について、$b_n=$$\underline{a_{n+1}+2a_n}$となる数列を考えると、左辺は$b_{n+1}$と置くことができます。つまり、

$b_{n+1}＝ 5b_n$

$n=1$のとき、$b_1=a_2+2a_1=1$より、$b_n=5^{n-1}$

つまり、$a_{n+1}+2a_n=5^{n-1} \cdots Ⅴ$

となります。同様に$Ⅳ$について、$c_n=$$\underline{a_{n+1}-5a_n}$となる数列を考えると、左辺は$c_{n+1}$と置くことができます。つまり、

$c_{n+1}＝ -2c_n$

$n=1$のとき、$c_1=a_2-5a_1=1$より、$c_n=(-2)^{n-1}$

つまり、$a_{n+1}-5a_n=(-2)^{n-1} \cdots Ⅵ$

$Ⅴ$と$Ⅵ$を連立方程式として解くと、

$a_n=\frac{1}{7}\lbrace5^{n-1}-(-2)^{n-1}\rbrace$

$Ⅰ$の数列の一般項$a_n$を求めることができました。
隣接三項間の漸化式では、このように特性方程式を利用して一般項を求めることができます。

フィボナッチ数列と黄金比の関係を表す証明

ここで本題のフィボナッチ数列と黄金比の関係性についての証明の話題に移りましょう。
フィボナッチ数列の漸化式 $F_{n+2}=F_n+F_{n+1}$ $(n≧0,\ \ F_0=0, \ F_1=1)$ は隣接三項間の漸化式なので、上記で説明した特性方程式を利用して一般項を求めることができます。

特性方程式の公式に当てはめると、$F_{n+2}-F_{n+1}-F_n=0$より、$x^2-x-1=0$
この2解が$\alpha, \beta$ $(\alpha≦\beta)$ のとき、

\begin{equation*}
\begin{cases}
F_{n+2}-αF_{n+1}=β(F_{n+1}-αF_n)\\
F_{n+2}-βF_{n+1}=α(F_{n+1}-βF_n)
\end{cases}
\end{equation*}

と変形できます。
ここでは「解の公式」を使用して、$\alpha, \beta$ の値を求めてみましょう。

解の公式

二次方程式 $ax^2+bx+c=0\ (a\neq 0)$ の2つの解は、

$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$

である。

解の公式に当てはめて解くと、$a=1, \ b=-1, \ c=-1$ なので、

$$x=\frac{1\pm\sqrt{1+4}}{2} = \frac{1\pm\sqrt5}{2}$$

$α≦β$より、$(α, \ β) = (\frac{1-\sqrt5}{2},\ \frac{1+\sqrt5}{2})$

$\alpha$と$\beta$の値を代入して解くこともできるのですが、分数や根号が出てきて計算がややこしくなるので、ここでは一旦$\alpha$と$\beta$のまま計算を続けてみましょう。

$F_{n+2}-\alpha F_{n+1}=\beta(F_{n+1}-\alpha F_n) \cdots ①$
$F_{n+2}-\beta F_{n+1}=\alpha(F_{n+1}-\beta F_n) \cdots ②$

ここで、$\bf{B_n}$$=F_{n+1}-\alpha F_n \cdots ③$、$\bf{C_n}$$=F_{n+1}-\beta F_n \cdots ④$となる数列を考えると
①と②の左辺は、それぞれ$\bf{B_{n+1}}$、$\bf{C_{n+1}}$と表すことができます。
したがって、次のように書き換えます。

$\bf{B_{n+1}=B_n}$$\times\beta \cdots ⑤$
$\bf{C_{n+1}=C_n}$$\times\alpha \cdots ⑥$

これは、等比数列の形$a_{n+1}=a_nr$と同じですね！

ここで、実際の値を$(\alpha, \ \beta) = (\frac{1-\sqrt5}{2},\ \frac{1+\sqrt5}{2})$として代入します。

$n=1$のとき、③より、$\bf{B_1}$$=1-\frac{1-\sqrt5}{2}\times 1=\frac{1+\sqrt5}{2}=\beta$

④より、$\bf{C_1}$$=1-\frac{1+\sqrt5}{2}\times 1=\frac{1-\sqrt5}{2}=\alpha$

となります。
このことから、⑤は初項が$\beta$、公比が$\beta$の等比数列、⑥は初項が$\alpha$、公比が$\alpha$の等比数列であるとわかり、等比数列の一般項$a_n$は、$a_n=a_1\times r^{n-1}$（$r$は公比）で表されるので、⑤、⑥はそれぞれ、

$\bf{B_n}$$=\beta^n \cdots ⑤’$
$\bf{C_n}$$=\alpha^n \cdots ⑥’$

と表すことができます。
これを③、④にあてはめると、

$\beta^n=F_{n+1}- \alpha F_n \cdots ⑦$
$\alpha^n=F_{n+1}-\beta F_n \cdots ⑧$

⑦、⑧を連立方程式として解くと、フィボナッチ数列の一般項$F_n$は、

$$F_n=\frac{\beta^n-\alpha^n}{\beta-\alpha}$$

と表されることがわかりました。

フィボナッチ数列の隣り合う2つの数の比は$\frac{F_{n+1}}{F_n}$で表せるので、

$$\frac{F_{n+1}}{F_n}=\frac{\frac{\beta^{n+1}-\alpha^{n+1}}{\beta-\alpha}}{\frac{\beta^n-\alpha^n}{\beta-\alpha}}=\frac{\beta^{n+1}-\alpha^{n+1}}{\beta^n-\alpha^n} \cdots ⑨$$

⑨に$(\alpha, \ \beta) = (\frac{1-\sqrt5}{2},\ \frac{1+\sqrt5}{2})$を代入すると、

$$\frac{F_{n+1}}{F_n}=\frac{\left(\frac{1+\sqrt5}{2}\right)^{n+1}-\left(\frac{1-\sqrt5}{2}\right)^{n+1}}{\left(\frac{1+\sqrt5}{2}\right)^n-\left(\frac{1-\sqrt5}{2}\right)^n}\ \cdots⑩$$

という式で表すことができます。
分数がたくさん入っていてとてもややこしいので、ここでは分母と分子の両方に$\frac{2^n}{(1+\sqrt5)^n}$という値をかけることにします。それぞれ分けて考えてみましょう。

まず分母は、

$$\left\{\left(\frac{1+\sqrt5}{2}\right)^n-\left(\frac{1-\sqrt5}{2}\right)^n\right\}\times\frac{2^n}{{(1+\sqrt5)}^n}$$

$$=\left\{\frac{{(1+\sqrt5)}^n}{2^n}-\frac{{(1-\sqrt5)}^n}{2^n}\right\}\times\frac{2^n}{{(1+\sqrt5)}^n}$$

$$=\fbox{$1-\left(\frac{1-\sqrt5}{1+\sqrt5}\right)^n$}$$

次に分子は、

$$\left\{\left(\frac{1+\sqrt5}{2}\right)^{n+1}-\left(\frac{1-\sqrt5}{2}\right)^{n+1}\right\}\times\frac{2^n}{{(1+\sqrt5)}^n}$$

$$=\left\{\frac{{(1+\sqrt5)}^n\times(1+\sqrt5)}{2^n\times2}-\frac{(1-\sqrt5)\times{(1-\sqrt5)}^n}{2^n\times2}\right\}\times\frac{2^n}{{(1+\sqrt5)}^n}$$

$$=\fbox{$\left(\frac{1+\sqrt5}{2}\right)-\frac{1-\sqrt5}{2}\left(\frac{1-\sqrt5}{1+\sqrt5}\right)^n$}$$

分母と分子を⑩の式に戻すと、

$$\frac{\left(\frac{1+\sqrt5}{2}\right)-\frac{1-\sqrt5}{2}\left(\frac{1-\sqrt5}{1+\sqrt5}\right)^n}{1-\left(\frac{1-\sqrt5}{1+\sqrt5}\right)^n}$$

ここで、

$$-1<\left(\frac{1-\sqrt5}{1+\sqrt5}\right)^n<1$$

であり、$n$の値が大きくなればなるほど、$\left(\frac{1-\sqrt5}{1+\sqrt5}\right)^n$の値は限りなく$0$に近づいていきます。
そこで、$n$の値が非常に大きいと仮定して、$\left(\frac{1-\sqrt5}{1+\sqrt5}\right)^n$に$0$をあてはめてみると、

$$\frac{F_{n+1}}{F_n}=\frac{\left(\frac{1+\sqrt5}{2}\right)-\frac{1-\sqrt5}{2}\left(\frac{1-\sqrt5}{1+\sqrt5}\right)^n}{1-\left(\frac{1-\sqrt5}{1+\sqrt5}\right)^n}$$

$$≒\frac{\left(\frac{1+\sqrt5}{2}\right)-\frac{1-\sqrt5}{2}\times0}{1-0}$$

$$=\frac{\left(\frac{1+\sqrt5}{2}\right)}{1}=\frac{1+\sqrt5}{2}$$

という、黄金比の値$\frac{1+\sqrt5}{2}$が出てきました。
このことから、フィボナッチ数列の隣り合う2項の比$\frac{F_{n+1}}{F_n}$は、黄金比$\ \frac{1+\sqrt5}{2}$に限りなく近づくということが証明できます。

ところで、⑩の式で分母と分子の両方に$\frac{2^n}{{(1+\sqrt5)}^n}$をかけましたが、代わりに$\frac{2^n}{{(1-\sqrt5)}^n}$をかけるとどうなるのでしょうか。これは、

$$\frac{F_{n+1}}{F_n}=\frac{\frac{1+\sqrt5}{2}\left(\frac{1+\sqrt5}{1-\sqrt5}\right)^n-\frac{1-\sqrt5}{2}}{\left(\frac{1+\sqrt5}{1-\sqrt5}\right)^n-1}$$

という計算結果になります。ここで$\left(\frac{1+\sqrt5}{1-\sqrt5}\right)^n$の値は、

$$\left(\frac{1+\sqrt5}{1-\sqrt5}\right)^n \ →\pm\infty$$

と、無限に大きくなる数字になります。この計算結果でも、$n$の値が大きくなればなるほど$\frac{F_{n+1}}{F_n}$は黄金比に近づいていくと考えられますが、数値が途方もなく大きくなるので、証明には不適切であると言えます。

もっと考えてみよう！

黄金比と同様に人間が美しいと感じる比率として、「白銀比」というものもあります。白銀比の比率は$1:\sqrt2$（近似値$1:1.414$）であり、黄金比と比べると比率は大きくありません。白銀比は、日本人に馴染みのある比率と言われており、有名なものだと「法隆寺」や「東京スカイツリー」などに使用されているそうです。白銀比は日本固有の美的価値観を表していると言われています。

＼ SNSでシェアしよう／