みなさんはいつのまにか数をあやつり、算数・数学の問題を解くときや、普段の生活の中で数を巧みに使いこなしています。数学が長い歴史を経て現在の形になったように、みなさんも子どもの頃から少しずつ数に触れて数学への理解を深めているのです。この記事では、数の概念と、数の世界の広がりについて紹介します。

集合数と順序数

突然ですが、小学1年生の時にどのような算数の勉強をしたか覚えていますか？はじめは「かず」について学びます。\(1，2，3，\cdots \cdots 10\)までの数字の書き方や読み方を学ぶのですが、ただ数を数えたり書いたりするのではなく、“数には役割がある”ということを学んでいました。

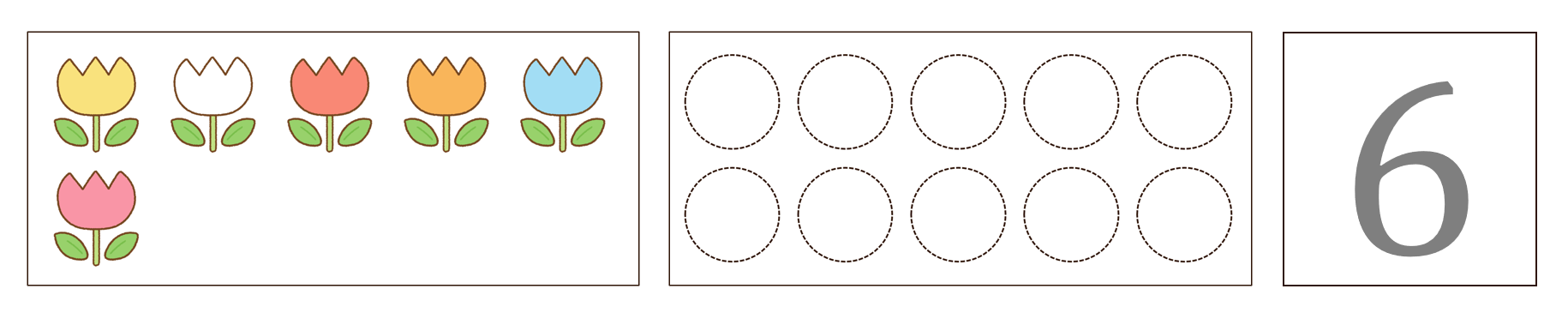
上の図は、「\(6\)」という数を知るための勉強です。多くの人にとって、「チューリップが\(6\)本ある」と言うことは、それほど難しいことではないでしょう。しかし、学校で学習する最初の算数の授業では、上の図を見ながら、「おなじ かずだけ ○に いろを ぬりましょう。」「すうじを かきましょう。」という勉強をします。

ここで大切なことは、チューリップと“同じ数だけ○をぬる”ということです。その理由の1つは、数え間違いを無くすことができるようになるためです。もう1つの理由は、○をぬることで、チューリップから離れて、数としての\(6\)をイメージできるようにするためです。

難しく言うと、「集合の要素（\(6\)本のチューリップ）と数詞（\(6\)）が1対1に対応」できるように工夫されているのです。

このようにしてまず1から10までの数字を学びます。

このとき学んだ数は「集合数(しゅうごうすう)」と言って、男子が\(6\)人、本が\(6\)冊、チョコレートが\(6\)個、……のように、ものの個数を表す役割としての数です。数を見て“多い”“少ない”という判断ができるのは、このような考えができているからです。

その次に学ぶのは、ものを並べると順番を考えることができること、つまり順番を表す役目としての数です。このような数を「順(じゅん)序数(じょすう)」と言います。

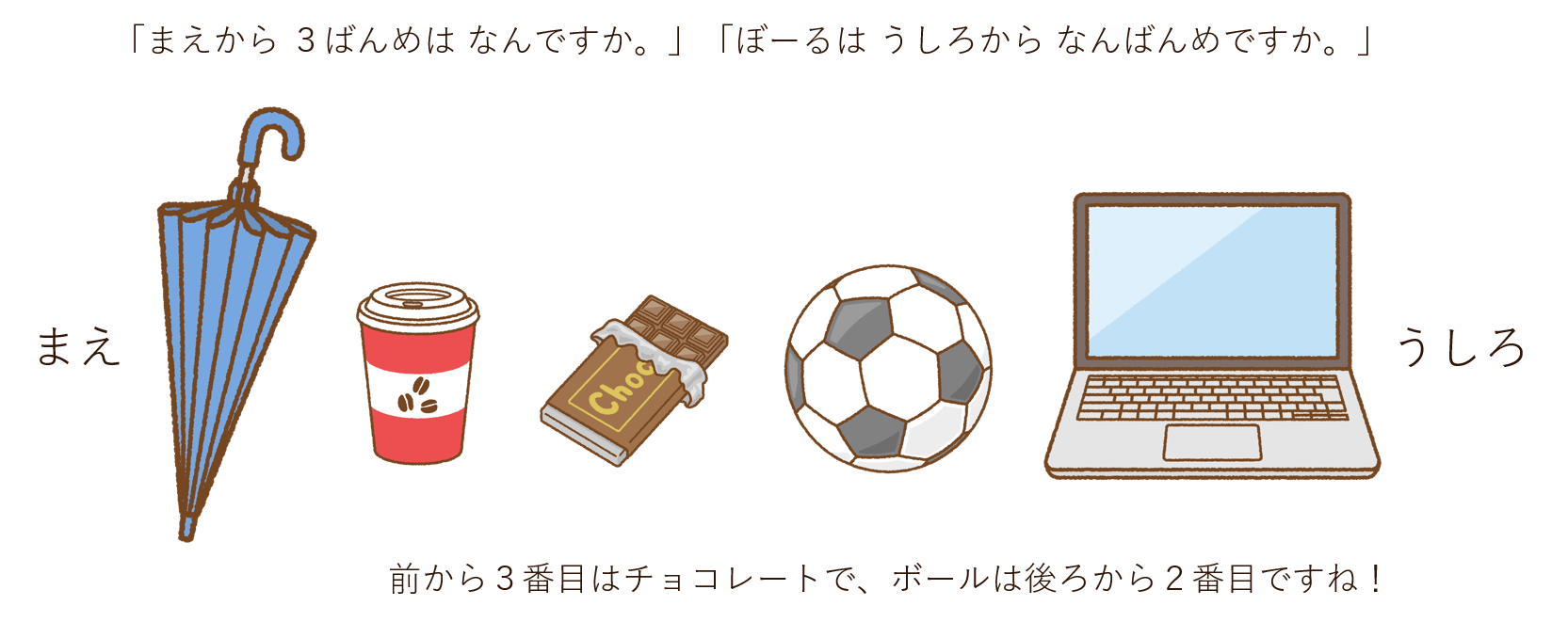
また、このような使い方を覚えることで、ものの「位置」を表すこと、その「位置」を人に伝えることができるようになります。たとえば、「前から\(3\)番目の椅子に座ってください」「右から\(2\)番目のお茶碗を使ってください」などのように用いられます。

「まえから \(3\)こ ぬりましょう」と「まえから \(3\)ばんめを ぬりましょう」では、同じ\(3\)を使っていながら、一方は「個数としての\(3\)」、もう一方は「順番としての\(3\)」と、それぞれ異なることを表しています。

数の世界の広がり

数の概念についてふり返ったところで、次は数の種類や歴史をご紹介します。「数」と聞くと、みなさんが思い出すのはどのようなものでしょうか。\(1，2，3，\cdots \cdots\)のような整数や、\(\frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \cdots \cdots\)のような分数でしょうか。実は数の世界には、日常生活では意識しない数がたくさん含まれています。ここでは順を追って、数の世界の広がりを紹介します。

0の発明

今から1300～1400年以上前に、\(0\)の概念がインドで発明されたと言われています。これによって、\(0～9\)までの十個の数字で、どんな数も表すことができる、位取(くらいど)り記数法(きすうほう) が可能になりました。

下のような古代エジプト数字やローマ数字では、\(10，100，\cdots \cdots\)になるごとに新しい記号を増やしていて、数字が大きくなるほど記号が増えていくので、特に大きな数を表すには不便だといえます。

これに対して、今日私たちが使っているアラビア数字であれば、\(0,\ 1,\ 2, \ 3, \ 4, \ 5, \ 6, \ 7, \ 8, \ 9 \)の\(10\)個の記号（数字）だけで、どんなに大きい数でも表すことができます。

アラビア数字で大きな数を書くときには、どのように書くでしょうか。普段は何気なく書いているかもしれませんが、どのような手順で書いているか思い出してみましょう。

まず、位(くらい)と呼ばれる数字を書く場所を考えます。いちばん右を一の位、その左を十の位、その左を百の位、…というように、それぞれの位は右の位のちょうど\(10\)倍の位として考えます。このように、\(10\)をひとつのまとまりとし、そのまとまりがさらに\(10\)集まると次の別のまとまりとして数える方法を十進法と言います。

位を考えたら、それぞれの位の場所に、その位のまとまりがいくつあるかを書きます。このとき、その位のまとまりが1つもなければ、その位に\(0\)を書きます。このように、\(0\)から\(9\)までの数字を横一列に並べて数を書き表す方法を十進(じゅっしん)位取(くらいど)り記数法(きすうほう)といいます。

紀元前に栄えたバビロニアでは、六十進位取り記数法に非常に近い数の書き方を使っていました。しかし、バビロニアには\(0\)がなかったため、\(0\)を書くかわりにその位には何も書きませんでした。このため、「\(1 \ \ 2 \ \ \)」と書いてあったとき、それは\(1020\)かもしれませんし、\(10020\)かもしれませんし、もしかしたら、\(102\)かもしれず、記法としては不完全だったのです。

位取り記数法で数を書くことの一番の利点は、位をそろえて書くことで、筆算ができるようになることです。\(0\)は、その位のまとまりがないことを表すだけの記号ではなく、ほかの数字とたしたりひいたりできる数字のひとつでした。\(0\)の発明によって筆算も発明されたのです。

特に大きな数同士のかけ算は、私たちが小学校で習うような、位取り記数法による筆算を使うことで、とても簡単に計算をすることができます。逆に、ローマ数字を使っていた13世紀より前のヨーロッパの人々は、計算が必要なときは、筆算ではなくローマ式のそろばんを使用するのが主流でした。

整数

先述した「集合数」や「順序数」で使用した、\(1，2，3，\cdots \cdots\)といった数のことを自然数と言います。

自然数には\(0\)も含まれそうですが、\(0\)は特別な数なので自然数に含めないことが多いです。

小学校1年生では、集合数と順序数の次にたし算とひき算を習いました。

自然数同士のたし算の答えは自然数になります。では、自然数同士のひき算の答えは、同じように自然数になるでしょうか。答えは、場合によります。ひく数がひかれる数より小さければ自然数になりますが、同じ数同士なら\(0\)になり、大きければ自然数にも\(0\)にもなりません。

ひく数がひかれる数より大きいときの計算の結果を表すためには、自然数と\(0\)以外の数を考えなければなりません。それは負の数（負の整数）です。負の数の登場は\(0\)の発明よりも早く、紀元前200年代の中国の「九(きゅう)章(しょう)算(さん)術(じゅつ)」という本で、すでに扱われていました。また5世紀頃のインドでは、負の数が負債や反対方向を表すものとして使われていました。

負の数と0と自然数を合わせて、整数とよびます。自然数は正の整数であるとも言えます。整数同士の計算を考えてみると、たし算、ひき算、かけ算の結果は整数になるといえます。

それでは、わり算の場合はどうなるでしょうか。
整数同士のわり算であっても、結果は整数にならないことがありますね。そこで、どんな整数同士のわり算も計算できるように、数の世界をもう少し広げてみましょう。

分数

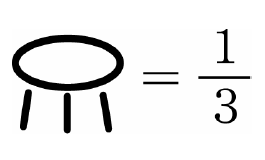
分数のはじまりは意外に早く、今から4000年前のエジプトで、すでに使われていたとされています。表し方は現在とは異なり、右のようなものだったそうです。

1500年前頃のインドでは、現在のように分母と分子を上下に書く書き方があり、1000年前頃のアラブで、現在の\(\frac{2}{3}\)のように分母と分子のあいだに線を書きはじめました。この書き方がヨーロッパで知られるようになったのは、13世紀初頭の数学者フィボナッチが、自身の書籍でアラビア数字による位取り記数法や現在のような分数の記法を紹介してからです。

小数

オランダの数学者ステヴィンが1585年に出版した「十進分数論」のなかで、はじめて小数を発表しました。ステヴィンの小数の表し方は、以下のようなもので、現在のように小数点を使った表し方になったのは、その20年後といわれています。

現在の表し方　\(2.135\)
ステヴィンの表し方　\(2⓪1①3②5③\)

日本では、江戸時代のはじめに中国から小数の考え方が伝わりました。このときは、

\(0.1＝\)一分　\(0.01＝\)一厘　\(0.001＝\)一毛　……

と表していました。これが、日本で昔から金利の単位として使われていた「割」と合わさり、利子計算に

\(0.1＝\)一割　\(0.01＝\)一分　\(0.001＝\)一厘　\(0.0001＝\)一毛　……

という数が使われるようになりました。これが野球の打率などを表すのに使われる歩合のもとになっています。

無理数

ここまで出てきた数は、すべて、整数や分数（分数で表される小数も含む）で表される数です。これらの数を「有理数(ゆうりすう)」といいます。たとえば、\(1\div3\)は、小数で表そうとすると、\(0.3333333 \ldots \ldots \)と終わりのない小数（無限小数）になりますが、分数では\(\frac{1}{3}\)と表すことができます。

しかし、円周率\(π \ (3.1415 \ldots \ldots )\)や、面積が\(2\)の正方形の1辺の長さである\(\sqrt2 \ (1.4142 \ldots \ldots)\)は無限小数になり、分数でも表すことができない数なのです。このような数を「無理数」といいます。この数を発見したのは、今から2500年程前の数学者ピタゴラスを中心とした学者の集団です。現在のように√を使って表したのは、17世紀のフランスの数学者デカルトが最初であると言われています。

\(\sqrt2\)は、簡単に実感することができます。

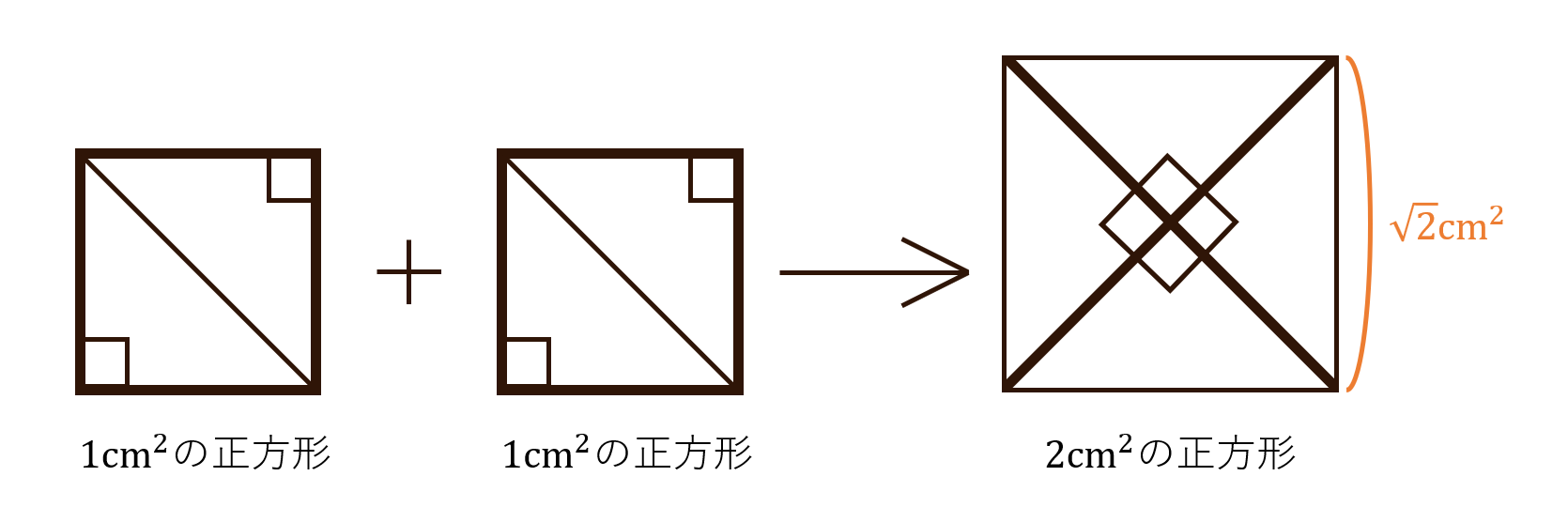
\(1{\rm cm}^2\)の正方形を2つ用意し、対角線で切って、それぞれ2つの直角三角形にします。できた4つの直角三角形を組み合わせると\(2{\rm cm}^2\)の正方形ができます。できた正方形の1辺の長さが\(\sqrt2 {\rm cm}\)です。

ここまで紹介した数の世界を、数直線を用いて表して見てみます。

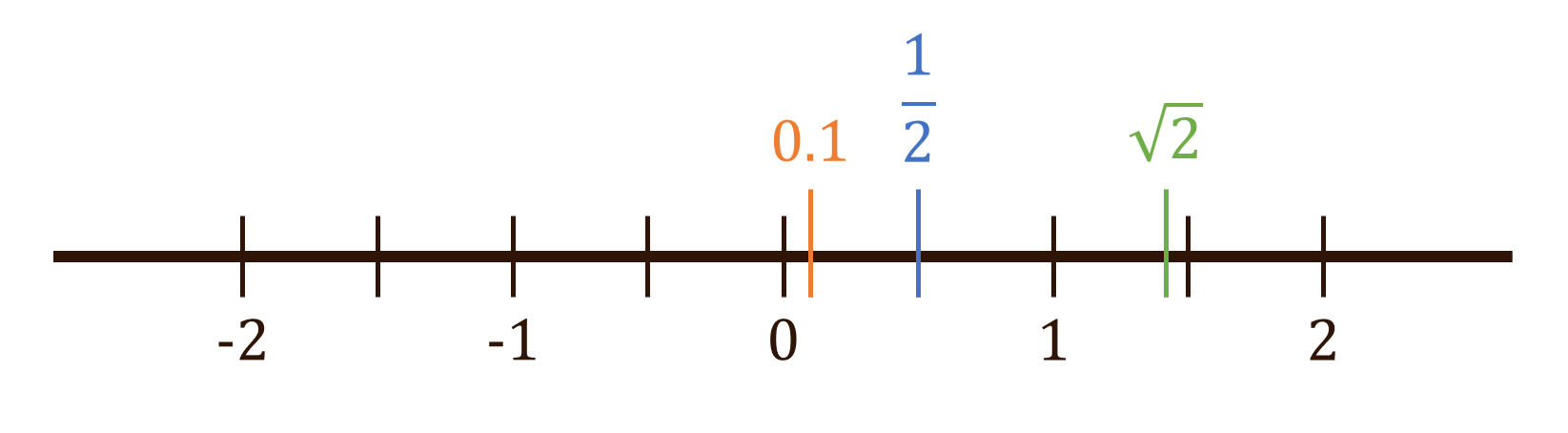
「√の数なんかなくても困らないんじゃないの？」と思う人もいるかもしれません。確かに、普段の生活では√の数を意識することは少ないでしょう。しかし、何気なくひいた数直線には、今まで紹介したすべての数が連続して存在しています。実は、数の世界はこれで終わりではありません。

実数と虚数

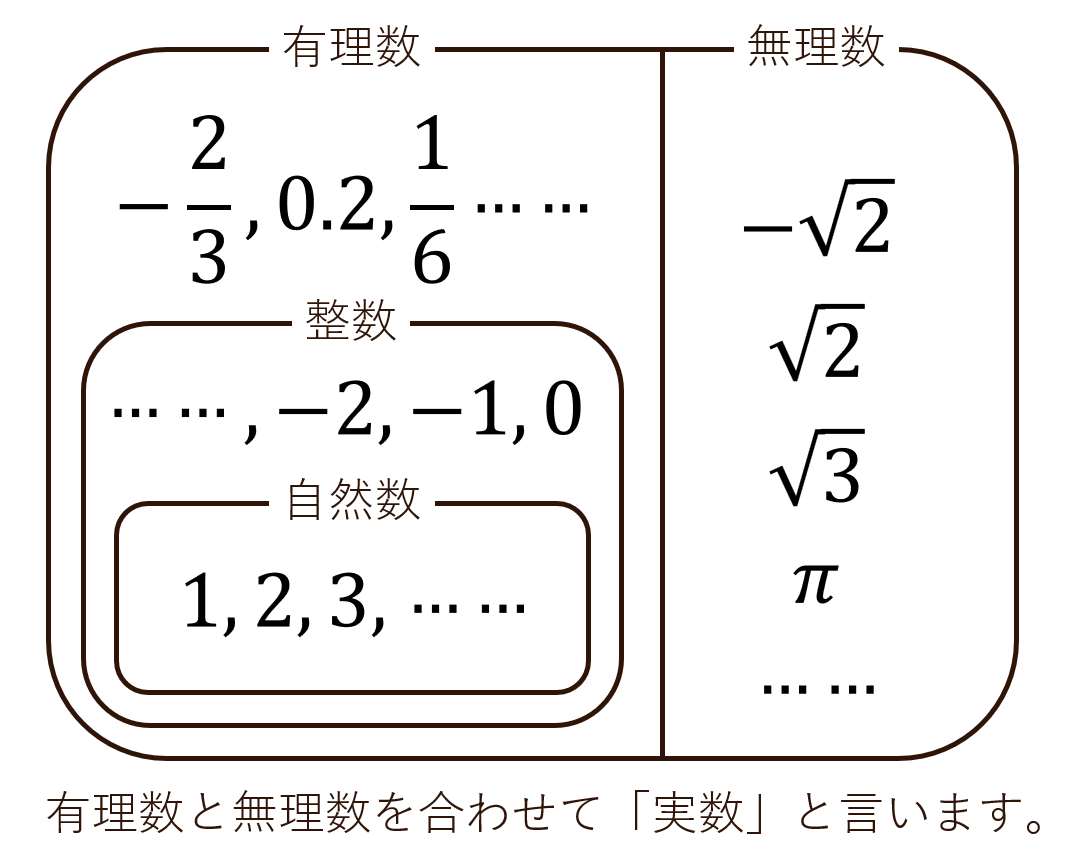
これまで紹介してきた内容は、すべて「実数」と呼ばれる、2乗すると必ず\(0\)以上になる数です。実数は数直線上に配置することができます。
一方、2乗して\(−1\)になる数 \(i\)（虚数単位）を使った虚数の世界というものも存在します。虚数は架空の数で、人間が作った理論上存在する大きさの見えない数です。虚数は、2乗すると必ずマイナスになります。また、実数のように数直線上に配置できません。

もっと考えてみよう！

虚数は実数と異なり、実際に存在しない理論上の数ですが、これらは自然や宇宙の世界を研究するのに用いられている数です。人間はこれらの数を駆使し、自然や宇宙の仕組みを研究し、その真理を探ってきました。みなさんの学習している数の世界は、決して学校の勉強だけの世界ではないのです。