算数・数学の世界　「物質の大きさと単位」

人類が数としてはじめに考えたものは、集合数と呼ばれる、ものを数えるための数でした。その後、負の数の存在に気がつき、やがて「\(0\)」を発明しました。「\(0\)」の発明によって、どんなに大きな数でも、\(0\)～\(9\)の10個の数字だけを使って書き表せるようになりました。

また一方で、ものを分けるための数として分数を発明しました。さらに、図形の中に円周率や\(\sqrt{ 2 }\)などの分数で表せない数、無理数が含まれていることを見つけました。そして、小数点の発明によって、どんな小さな数も書き表せるようになりました。また、加えて自然や宇宙への理解を深めるために、実際には存在しない理論上の数である虚数も扱うようになりました。

ここまでの内容を【算数・数学の世界】「どんどん広がる数の世界」でご紹介しました。

とても大きな数や、とても小さな数は、今日ではどのような場面で、どのように使われているのでしょうか。
この記事では、物質の大きさくらべを通して、より大きな数字の単位と、それが使われる物質世界の広がりをご紹介します。

物質の大きさ

原子

物質をどこまでも分解していくと、最後には、化学反応ではこれ以上分解できない原子と呼ばれる粒にたどり着きます。原子は、物質をつくるもととなる粒子です。原子の大きさや質量は種類によって異なり、すべての物質は原子からできています。

原子には、

1. 化学反応では、それ以上分けられない
2. 化学反応では、新しくできたり、ほかの原子に変わったり、なくなったりしない
3. 種類によって大きさや質量が決まっている

という性質があります。

分子

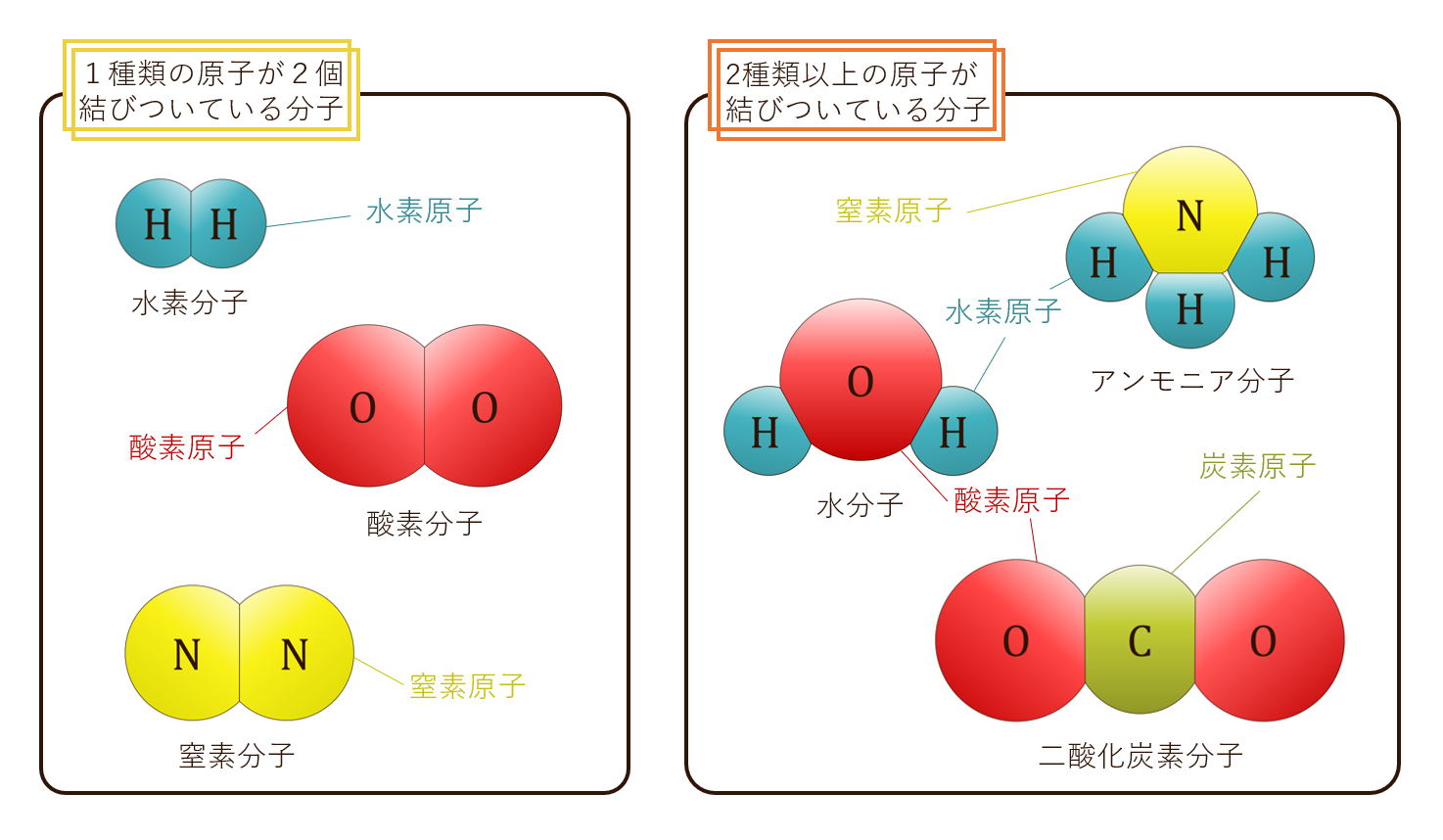
分子とは、原子が結びついてできた粒子のことで、物質の性質を表す最小の単位です。1種類の原子だけからできている分子と、2種類以上の原子からできている分子があります。例えば、酸素分子は酸素原子が2個結びついている分子ですが、水分子は酸素原子と水素原子という2種類の原子が結びついている分子です。

例えば、1円玉はアルミニウム原子からできています。1つの1円玉に含まれるアルミニウム原　　子の個数はおよそ22,000,000,000,000,000,000,000個（220垓がい個）です。1秒間に1個ずつ数えた場合、数え終わるまでに697,137,931,908,637年（約700兆年！） かかる計算になります。

大きな数の単位

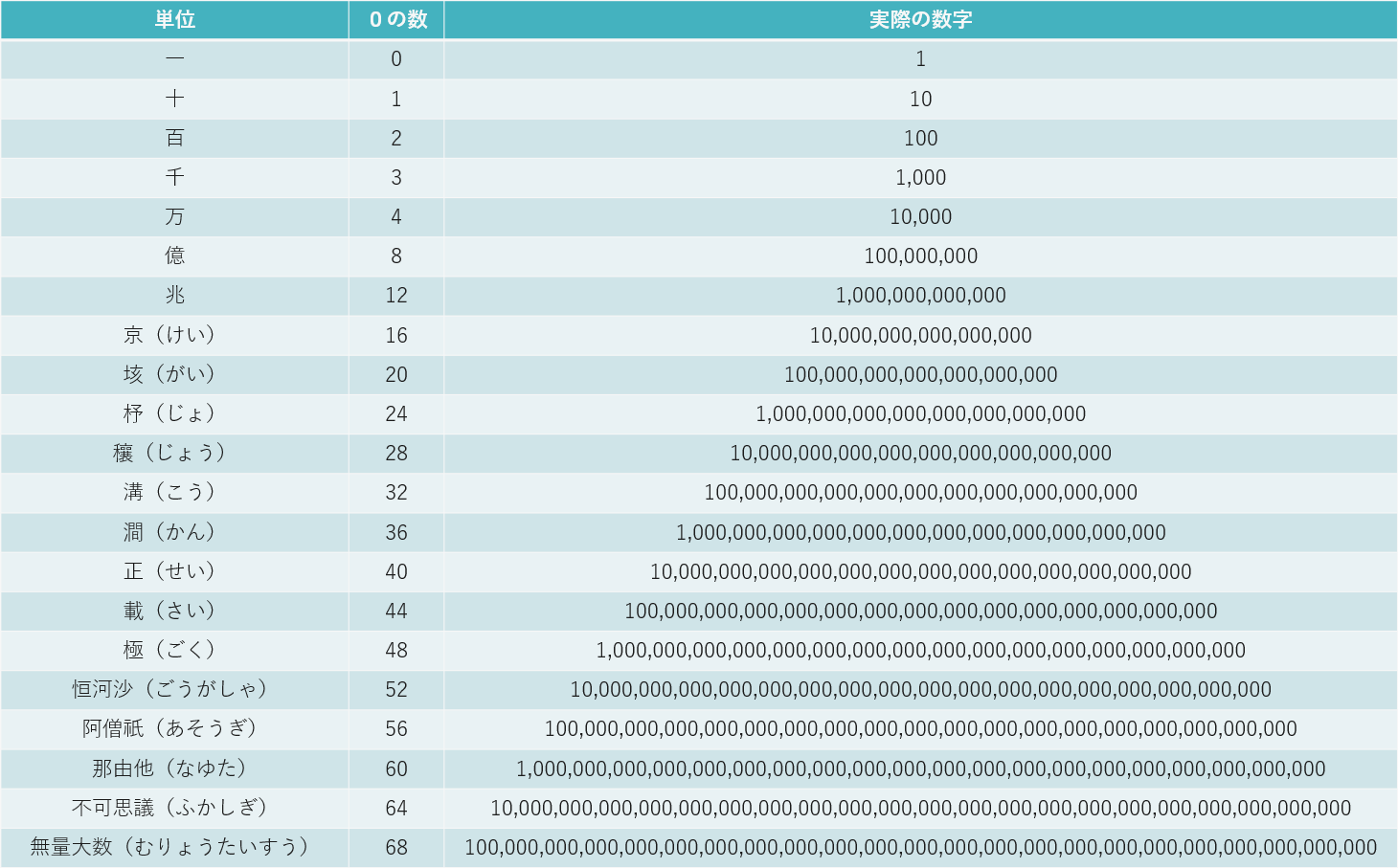
ところで、220垓なんて聞いたこともない単位ですね。大きな数は、日本語でどのように数えるのでしょうか。日本語での数の大きさの単位と実際の数字を、表で示します。

物質世界の大きさくらべ

以下の表は、原子のサイズから地球のサイズまでを下から順にならべたもので、上の段にいくにしたがって10倍ずつ大きくなり、下の段にいくにしたがって\(\frac{1}{10}\)倍ずつ小さくなっています。原子や分子はいちばん下の方の段です。ウイルスから3つ上の段にのぼるとアメーバとなり、アリから3つ上の段にのぼるとクジラになるのは、ウイルスとアメーバの大きさの比は、アリとクジラの大きさの比と同じイメージであるということです。水分子から8段のぼるとリンゴになり、リンゴから8段のぼると地球になっています。つまり、1つの水分子をリンゴの大きさに拡大させると、リンゴは地球の大きさになるということです。

累乗と指数

数が大きくなったり小さくなったりすると、その数字を書くだけでも一苦労です。もっと数をコンパクトに書く方法として累乗るいじょうをご紹介します。同じ数をいくつかかけ合わせたものを、その数の累乗、かけ合わせた個数を指数しすうといいます。

\(2+2+2＝2\times3\) というように、同じ数を何度も“たす”場合は、かけ算を使うと簡単に書けます。では、同じ数を何度も“かける”場合はどうでしょうか。このようなときは、累乗を使うと簡単に書くことができます。
例えば 、\(2\times2\times2\) を累乗の書き方で書いてみましょう。\(2\times2\times2\) は、\(2\) を \(3\) 回かけています。このときは、\(2\) の右上に小さく \(3\) と書きます。つまり \(2^3\) です。これは、「\(2\) の \(3\)乗じょう」と読みます。
逆に、累乗の書き方で書いてあるものをかけ算の形に戻すときは、左の数を右上の数だけ並べてかけます。例えば、\(5^4\) は、\(5\) を \(4\) 回かけるので、\(5\times5\times5\times5\)です。また、累乗の書き方をしたときに、左にある数を「底てい」、右上の小さく書かれた数を「指数」と言いいます。\(8^2\)であれば、底が \(8\) で指数が \(2\) です。
指数を使えば、1つの1円玉に含まれるアルミニウム元素の個数は \(22\times10^{22}\) と書くことができますし、1無量大数は \(10^{68}\) と書くことができます。このように、とても大きな数を表すときは、累乗の書き方を使うことでコンパクトに書くことができます。

指数法則

同じ数を何度もかける計算は、累乗の書き方にしても、すぐに計算できるわけではありません。そこで、累乗の書き方を使って計算できる指数法則という計算方法を、4つご紹介します。指数法則をうまく使うと、かけ算やわり算を、たし算やひき算の考え方で計算できるので、計算がとても簡単になることがあります。

①　\(a^n \times a^m = a^{n+m}\)
底が同じ累乗のかけ算は指数のたし算である、という法則です。
例として、\(5^4\times5^3\) という計算を考えてみましょう。
\(5^4\times5^3 = (5\times5\times5\times5) \times (5\times5\times5) = 5\times5\times5\times5\times5\times5\times5 = 5^7\) となり、答えは指数のたし算 \((3+4)\) の答えである\(7\)乗になりました。

②　\(a^n \div a^m = \frac{a^n} {a^m} = a^{n-m}\)
底が同じ累乗のわり算は指数のひき算である、という法則です。
例として、\(4^5 \div 4^3\) を考えてみましょう。
計算すると、\(4^5 \div 4^3 = \frac{4 \times 4 \times 4 \times 4 \times 4} {4 \times 4 \times 4} = 4^2\) となり、答えは指数のひき算 \((5-3)\) の答えである\(2\)乗になりました。

③　\({(a^n)}^m = a^{n \times m}\)
累乗の累乗は指数のかけ算である、という法則です。
例として、\({(2^4 )}^3\) を考えてみましょう。
これは、初めて見るとわかりにくいですが、底が \(2^4\) で指数が \(3\) の累乗です。かけ算の形にしてみましょう。
\({(2^4)}^3 = 2^4 \times 2^4 \times 2^4\)
\(=(2 \times 2 \times 2 \times 2)\)
\( \times (2 \times 2 \times 2 \times 2)\)
\( \times (2 \times 2 \times 2 \times 2)\)
\(= 2^{12}\)
上のように書いてみると、かけられている \(2\) は最終的に \(4 \times 3 ＝ 12\)（個）です。

ここまでは、底が同じ累乗のかけ算やわり算について見てきましたが、底が違うけれど指数が同じ場合に利用できる法則もあります。

④　\(a^n \times b^n = {(a \times b)}^n\)
指数が同じ累乗の積は底の積であるという法則です。
例として、\(2^4 \times 3^4\) を考えてみましょう。式で書くと、
\({2^4} \times {3^4} = (2 \times 2 \times 2 \times 2) \times (3 \times 3 \times 3 \times 3)\)
\(= (2 \times 3) \times (2 \times 3) \times (2 \times 3) \times (2 \times 3)\)
\(= {(2 \times 3)}^4\)
\(= 6^4\)
となります。

ここまでのまとめを以下に示します。

指数の拡張

ここまで、指数は自然数であるとして考えてきました。
でも法則②で、指数同士のひき算の結果が自然数にならなかったら、どうすればいいでしょうか。
例えば\(4^3 \div 4^3\)を法則②のとおりに計算すると、\(4^3 \div 4^3=4^{3-3}=4^0\) となります。
累乗の記号は底を指数の回数かけ合わせたものだったので、\(4\)の\(0乗\)は\(4\)を\(0回\)かけたものになります。この数は、いくつでしょうか。

次の図のように考えてみましょう。

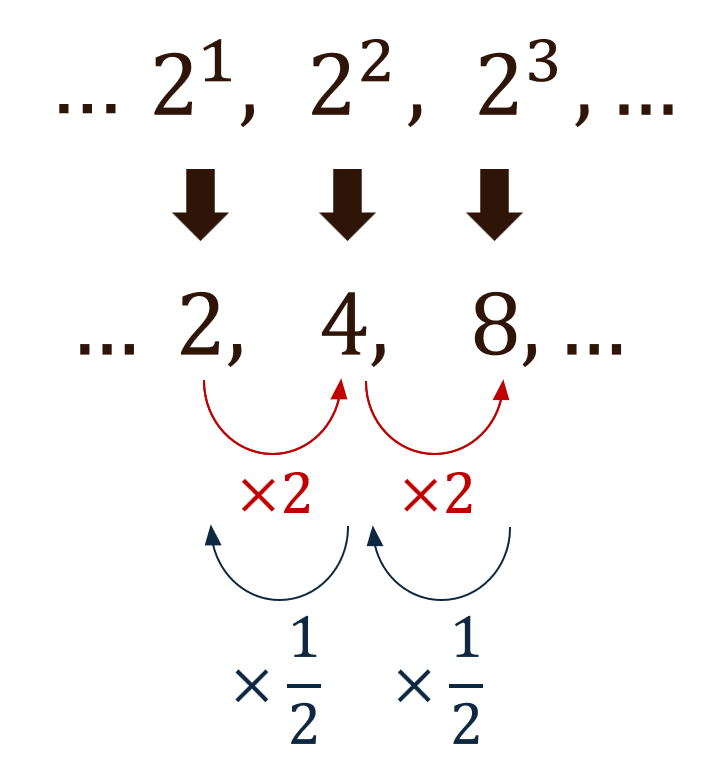
図のように、\(2^1\),  \(2^2\),  \(2^3\),  …となるとき、数は2倍すると右隣の値になりました。同じように考えると、\({1}{2}\) 倍すると左隣の値に変化することがわかります。
そこで、下の図のように考えると、… \(2^{-3}\), \(2^{-2}\), \(2^{-1}\),  \(2^0\) となるときの値についても考えることができます。

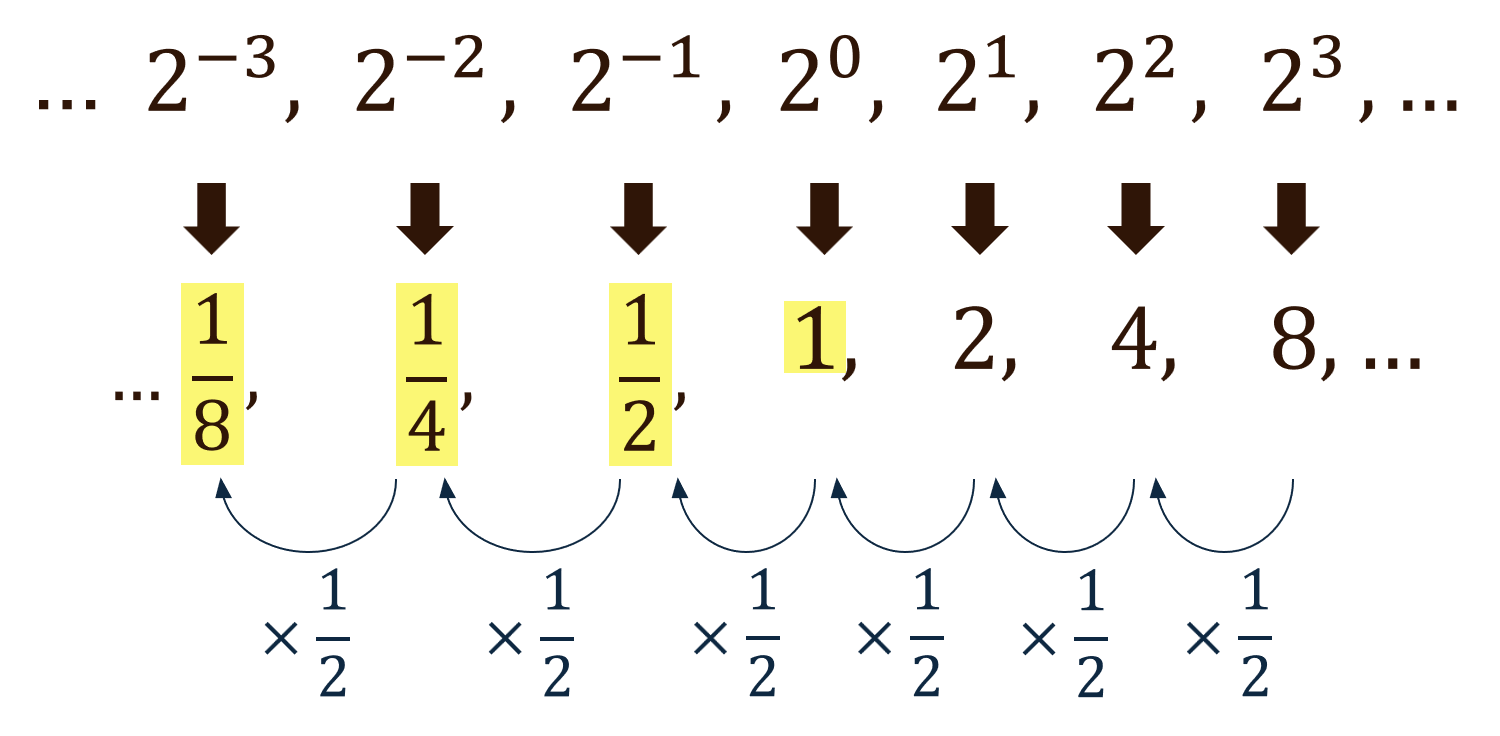
例えば、\(4^3\div4^3=4^{3-3}=4^0\) を法則を使わずに計算すると、\(4^3\div4^3=\frac{4^3}{4^3} =1\) になり、上の図の考え方が正しいことがわかります。

指数が分数になることもあります。

例えば、平方根 \(\sqrt{2}\) を考えてみましょう。
\(\sqrt{2}\) は2乗すると \(2\) になる値です。つまり、
\((\sqrt{2})^2 =2\) … \(A\)

では、\(2^\frac{1}{2}\) を考えてみましょう。この値を2乗すると、どのような値になるでしょうか。
指数法則の③を利用すると、
\((2^\frac{1}{2})^2 = 2^{\frac{1}{2} \times 2} = 2^1\) … \(B\)
であることがわかります。

\(A\)、\(B\)から、
\((2^\frac{1}{2})^2 = {(\sqrt{ 2 })}^2\)
\(2^\frac{1}{2} = ±\sqrt{ 2 }\)
となりますが、\(2^\frac{1}{2}\) は \(\sqrt{ 2 }\) と \( – \sqrt{ 2 }\) のどちらでしょうか。それとも、両方なのでしょうか。
このような混乱を防ぐために、底が正のときだけ指数が分数になることに決めましょう。そうすると、\(2^\frac{1}{2}\) は正の数なので、
\(2^\frac{1}{2} = \sqrt{ 2 }\) … \(C\)
であることがわかります。

一般に、\(a \gt b\) のとき、\(n\) 乗して \(a\) になる正の数を \(\sqrt[n]{ a }\) で表します。つまり、\(\sqrt{ 2 }\) は2乗して \(2\) になる正の数なので、\(\sqrt[2]{ 2 }\) と表されますが、指数を省略して \(\sqrt{ 2 }\) と表します。
ここで、3乗して \(2\) になる数は \(\sqrt[3]{ 2 }\)、4乗して \(2\) になる数は \(\sqrt[4]{ 2 }\) と表されます。
このことから、\(C\) と同じように考えると、
\(2^\frac{1}{3} = \sqrt[3]{ 2 }\)、\(2^\frac{1}{4} = \sqrt[4]{ 2 }\) と表すことができます。

実は、底が負のときでも、指数が奇数であれば、累乗を考えることができます。
例えば、\((-1)^\frac{1}{3}\) は3乗すると\(-1\)になる数なので、\(-1\)であることがわかります。つまり、\((-1)^\frac{1}{3} = \sqrt[3]{ -1 } = -1\) です。しかし、\((-1)^\frac{1}{4}\) は、4乗すると\(-1\)になる数ですが、そのような実数は存在しません。
このように、底が負になるとその累乗があったりなかったりするので、指数が分数になる可能性があるときだけ、底は正であるとします。

ここまでのまとめを以下に示します。

問題に挑戦！

今、1杯のコップの中に水が入っていて、その水を地球上のどこかに全部捨てたとします。捨てた水は年月を経て、地球上のあらゆる水のある場所に均一に広がったとします。そして、あらためてコップに同じ量の水を注ぎます。このコップの中の水の中には、はじめに捨てた水に入っていた水の分子が入っていると言えるでしょうか。入っているとしたら、何個くらいなのでしょうか。コップ1杯の水の中の水分子の数を \(5 \times 10^{24}\) 個、地球上に存在するすべての水分子の数を \(5 \times 10^{47}\) 個として求めてみましょう。

解答

コップの中の水に捨てた水の水分子が入っている確率は、\((5 \times 10^{24}) \div (5 \times 10^{47}) = (5 \div 5) \times 10^{24-47} =10^{-23}\)
コップの中の水分子の数は \(5 \times 10^{24}\) 個だから、\(5 \times 10^{24} \times 10^{-23} = 5 \times 10^{24-23} = 5 \times 10 = 50\)
よって、「コップに再び注いだ水の中には、はじめに捨てた水に入っていた水分子が \(50\) 個くらい入っている」と言えます。