今日、日本の学校で教えている算数や数学は、西欧で発達したいわゆる西洋数学です。では、西洋数学が伝わる前の日本では、どのようにして算数や数学の問題を解いていたのでしょうか。
西洋数学が伝わる前の日本では、和算と呼ばれる数学を使っていました。この記事では、小学生を教える先生方に向けて、和算の問題をいくつか紹介しています。また、中学生以上を教える先生方に向けて、和算と方程式の関係も紹介しています。授業の導入などにお使いください。
和算の歴史
日本には、飛鳥・奈良時代に、中国から初めて数学が伝わったとされています。この時期の数学は、一部の役人のみが学ぶものとされていました。室町時代になると、そろばんが中国から伝来し、商人など日常的に計算をする人たちも現れてきましたが、学問としての数学はまだ発達しませんでした。
数学が日本で学問として広がり、多くの人が数学を学びだしたのは、江戸時代になってからです。江戸時代になると、普通の人々も商売や生活をするための計算力・学力が必要になってきて、寺子屋などで勉強するようになりました。人々の教育や学問に対する関心も高まり、数学を教えたり、学んだり、研究したりする人々が生まれ、日本における学問としての数学が発達していきました。
この時代は、一部の国を除き外国との交易がありませんでしたので、数学も日本独自に発達していくことになります。後に外国から伝わる数学を「洋算」、それに対して日本の数学を「和算」と呼ぶようになります。
この時代の和算で興味深いのは、生活に密着した題材を使った問題が多く作られ、人々の娯楽としての一面もあったことです。ここでは、パズルのようで楽しい代表的な和算の問題をご紹介します。
つるかめ算
<問題>
鶴の足は2本で、亀の足は4本です。鶴と亀が合わせて10います 。足が全部で28本あるとき、鶴は何羽いますか?
<解答>
亀ばかりが10匹(鶴は0羽)いるとすると、足の数は \(4 \times 10=40\)(本)になります。
亀を1匹減らし9匹にして、鶴を1羽増やすと、足の数は \(4 \times 9+2 \times 1=38\)(本)になります。
つまり、鶴の数を1増やす(=亀の数を1減らす)ごとに、足の数は2本(=鶴と亀の個体の足の数の差)減ります。
実際には足は28本あるので、亀ばかりが10匹(鶴は0羽)いるときとの差は、\(40-28=12\)(本)です。
この差を、鶴と亀の個体の足の数の差 \(4-2=2\) で割れば、鶴の数が求められます。
つまり、足12本分を減らすには、鶴を何羽増やせばいいかを考えます。
よって、\((4×10-28)÷(4-2)=6\)(羽)
これが、鶴の数となります。
つるかめ算と方程式
つるかめ算の問題は、方程式を使って解く方法もあります。和算の解き方と全く異なる方法で解いているのに、同じ答えが出るのはなぜでしょうか。本当に全く違うことをしているのでしょうか。
<方程式を使った解き方>
鶴を\(x\)羽とすると、亀は \(10-x\)(匹)になる。
鶴の足は2本だから、鶴の足の合計は \(2x\)(本)
亀の足は4本だから、亀の足の合計は \(4(10-x)\)(本)
鶴の足の合計+亀の足の合計=28 → \(2x+4(10-x)=28\)……① という方程式ができます。
この方程式を解くと、
\(2x+40-4x=28\)
\(-2x=28-40\)
\(-2x=-12\)
\(x=6\)
となるので、鶴が6羽とわかります。
和算の解き方と比べるために、方程式①を次のように変形してみましょう。ここでは、あとで比べやすいように、あえて、たし算やかけ算を計算しないまま書いています。
まず、かっこを外すと、\(2x+4×10-4x=28\) になります。
この方程式の両辺から \(4×10\) を引くと、\(2x-4x+4×10-4×10=28-4×10\) ですね。
さらに、この式の両辺を\(-1\)倍すると、\(4x-2x=4×10-28\) になります。
左辺の\(x\)の項をまとめると、\((4-2)x=4×10-28\) と変形できます。
さらに、この式の両辺を\((4-2)\) で割ると、\(x=(4×10-28)÷(4-2)\) と変形できました。
この式の右辺は、和算で解いたときの式と全く同じです。
旅人算
<問題>
弟は家を出て、毎分50mの速さで学校に向かいました。8分後、弟の忘れ物に気付いた兄は、毎分150mの速さで弟を追いかけました。兄は家を出てから何分後に、弟に追いつきますか。
<解答>
兄が家を出るとき、弟は8分間歩いていたから、
2人の差は \(50×8=400\)(m)ひらいている。
弟は毎分50m、兄は毎分150mの速さで進むから、
1分間に2人の差は \(150-50=100\)(m)ずつ縮まる。
よって、\(50×8÷(150-50)=4\)(分後)に、兄は弟に追いつく。
旅人算と方程式
上の旅人算の問題も、同じように方程式を使って解いてみて、その解き方と和算の解き方を比べてみましょう。つるかめ算のように、和算で解いたときと同じ式があらわれるでしょうか。
<方程式を使った解き方>
兄は、家を出てから\(x\)分後に弟に追いつくとする。
追いつくまでに、兄は\(x\)(分間)歩いているので、\(150x\)(m)進む。
追いつかれるまでに、弟は \(x+8\)(分間)歩いているので、\(50(x+8)\)(m)進む。
「追いつく」ということは「2人の進んだ道のりが同じ」ということだから、
兄の進んだ道のり=弟の進んだ道のり → \(150x=50(x+8)\)……① という方程式ができる。
この方程式を解くと、\(x=4\)となるので、\(4\)(分後)に兄は弟に追いつく。
つるかめ算のときと同じように、方程式①を、たし算やかけ算を計算しないままにして変形してみましょう。
まず、かっこを外すと、\(150x=50x+50×8\)ですね。
次に、\(50x\) を移項すると、\(150x-50x=50×8\) となり、この式の左辺の\(x\)の項をまとめると \((150-50)x=50×8\)となりますね。
この式の両辺を \((150-50)\) で割ると、\(x=50×8÷(150-50)\) という式に変形できます。
この式の右辺も、やはり和算で解いたときと全く同じ式になりました。
和算のよさ、方程式のよさ
このように、和算を使って解いても、方程式を使って解いても、最終的には同じ計算をしています。みなさんは、和算と方程式のどちらの解き方に“よさ”を感じましたか?
和算では、「ひき算の結果の差は何の数を表しているのか」などを考えながら解く必要があります。そのため、扱っている数を具体的にイメージしやすいというよさがあります。
また方程式では、数量の関係をとらえて立式してしまえば、あとは形式的に計算するだけ、という非常に合理的なよさがあります。これは文字を使うことを学んだよさと言えます。
文字を使うよさは、今回の方程式だけでなく、今後の数学の学習の場面で感じることができるでしょう。
盗人隠し
<問題>
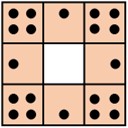
上の図のように、8つのマス目に合計20個の石が置いてある。
この石の置き方は、下の図を見ればわかるように、連続して隣り合う3つのマスに置いてある石の個数の和が、どれも9個になるようにしてある。

ここに、さらに石を6個増やして合計26個の石を置きたい。20個のときと同じように、連続して隣り合う3つのマスに置いてある石の個数の和が、どれも9個になるような置き方はあるか。
<解答>
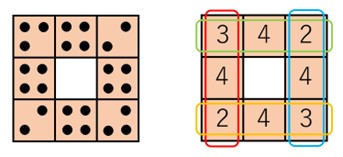
左側の図の置き方が正解です。右側の図は、確かめやすいように、置いてある石の数を数字で記したものです。マス目に置いた石の総数は6個増えていても、どの隣り合って並ぶ3マスの数字の和も9のままで、合計20個のときと変わらないことがわかりますね。
このように、数の配列・配置を変えて全体の数の増減をごまかすパズルを「盗人隠し(ぬすっとかくし)」といいます。
下に並んだ7つの図も、すべて一辺の3マスの数の合計が9になっています。では、この中で、8つのマス目の数を足し合わせた合計が最も大きいものはどれでしょうか。また、すべての数の和が同じ数になる図はあるでしょうか。
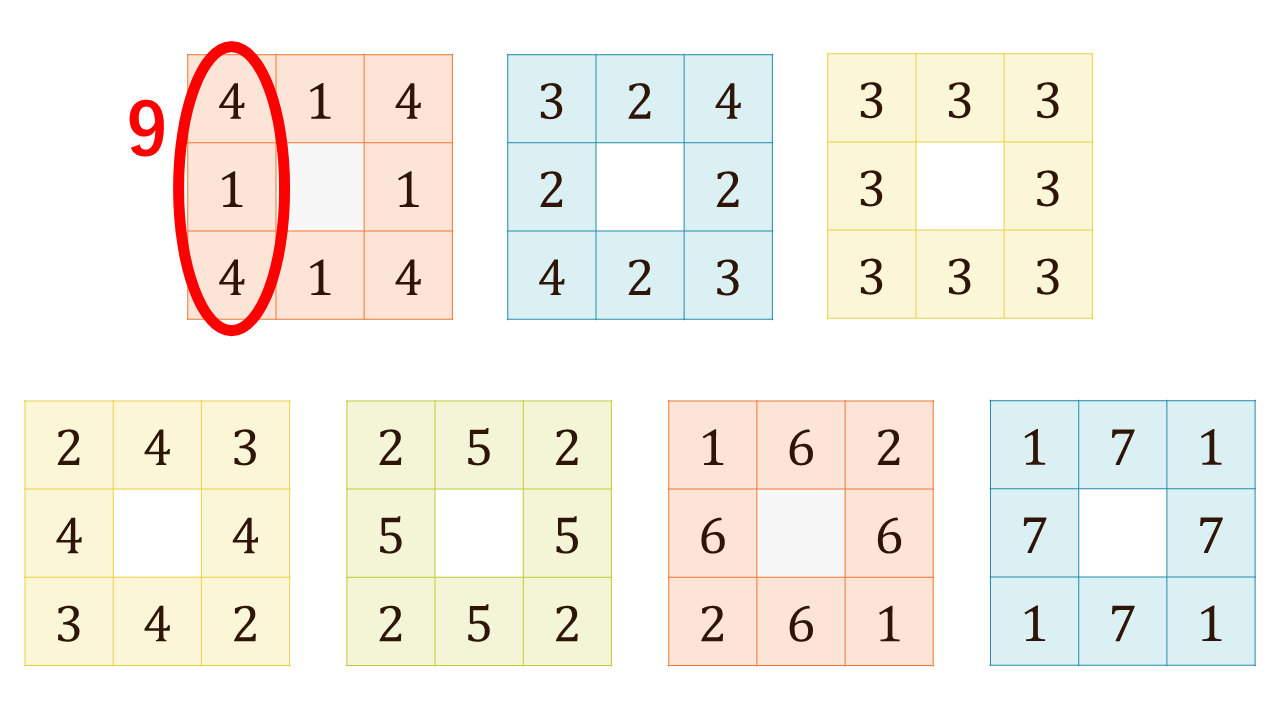
答えは、マス目の数の合計は、右下の図が一番大きくなります。また、すべての数の和が同じになる図はありません。なんと、合計数が一番小さなものと一番大きなものとの間で、12も差があります。一見同じように思える数字を、それだけごまかすことができるのです。
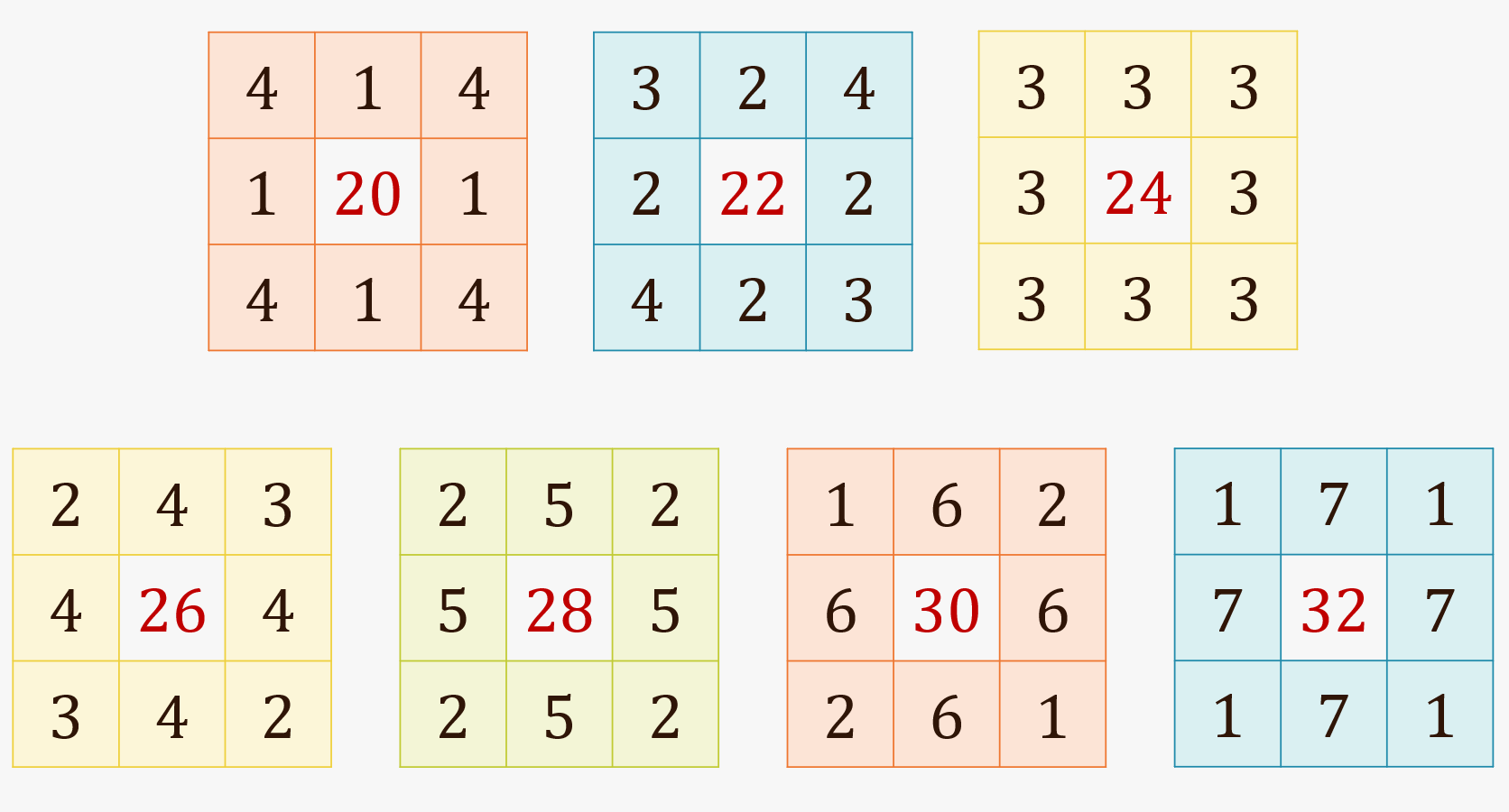
では、なぜこのようなことが起きるのでしょうか。それは、数字の配置に関係しています。一辺ずつ(隣り合って並ぶ3マスの)数の合計を数えるときに、この図の形(正方形)だと、辺の両端(つまり四隅)の計4つのマスの数字は2回ずつ数えることになります。
そのため、各辺の両端(つまり四隅)のマスの数字が小さくなればなるほど、各辺の真ん中のマスの数字が大きくなっていき、8つのマス目の合計数は大きくなるのです。
油分け算
<問題>
1斗桶の中に油が1斗 (1斗=10升、1升は約1.8L) 入っています。この油を、7升枡と3升枡の2つの枡を使って5升ずつに分けるには、どのようにすればよいでしょうか。
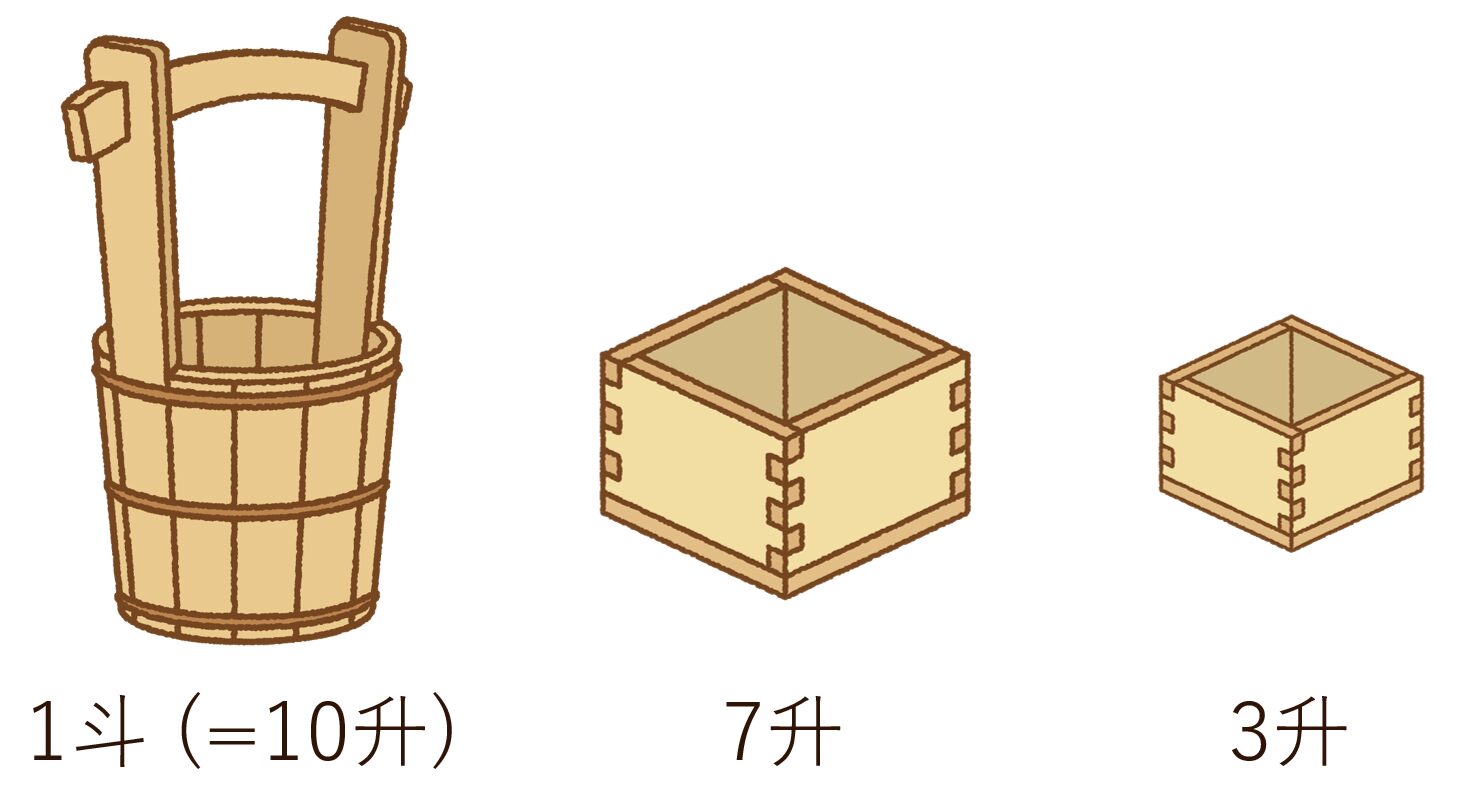
油分け算のルールは、桶と枡(容器)には目盛りがなく、その容器を満たしたときだけ油の容量がわかるということです。
油分け算は、グラフで視覚化して考えるとわかりやすくなります。
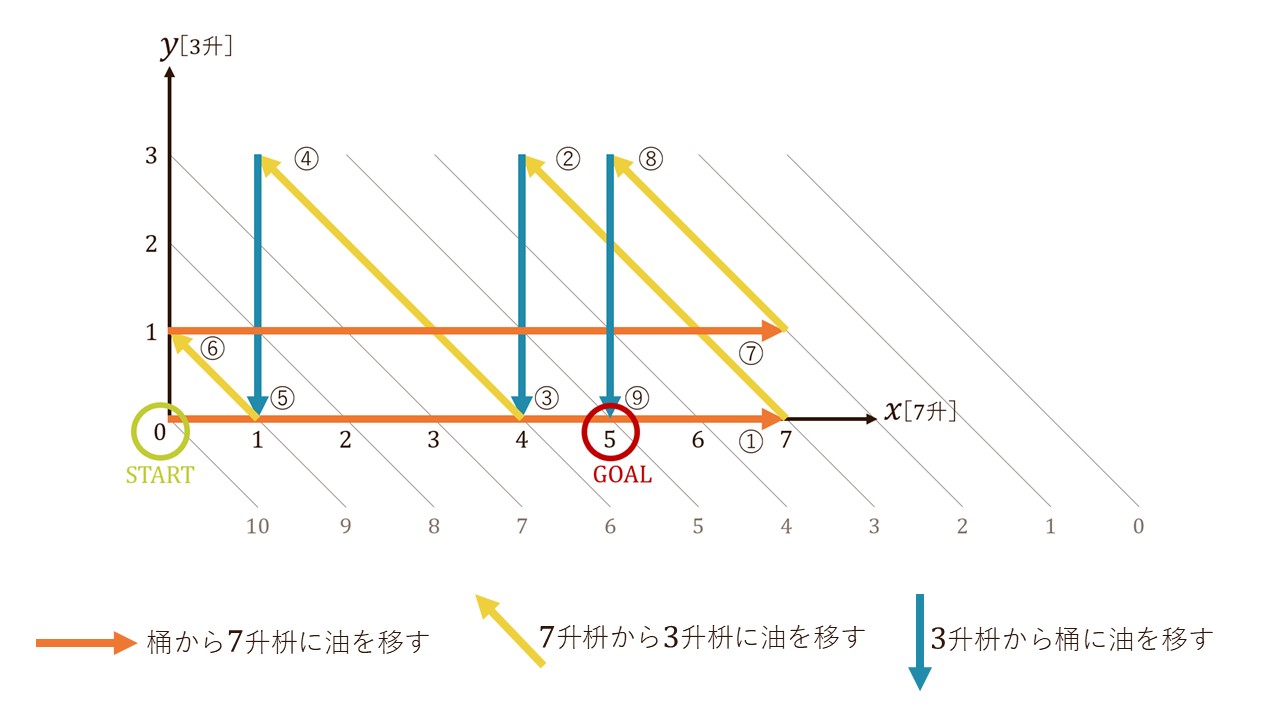
グラフ中の数字は各枡と桶の中に入っている油の量、矢印はそれぞれの油の動きを表しています。
x軸は7升枡、y軸は3升枡、斜めの線は桶に入っている油の量を表しています。出発点はグラフのSTARTの位置で、目的地はGOALの位置です。移動は、直線上 を進めるところまで進み、途中で止まることはできません。
| 最初の状態を (1斗桶=10, 7升枡=0, 3升枡=0) と表します。 | \((10, 0, 0)\) |
| ①まず、桶から7升枡に油を移します。 | \((3, 7, 0)\) |
| ②次に7升枡から3升枡に油を移します。 | \((3, 4, 3)\) |
| ③3升枡から桶に油を移します。 | \((6, 4, 0)\) |
| ④再び7升枡から3升枡に油を移します。 | \((6, 1, 3)\) |
| ⑤再び3升枡から桶に油を移します。 | \((9, 1, 0)\) |
| ⑥7升枡から3升枡に油を移します。このとき、7升枡に 油は1升残っているので、これを3升枡に移します。 |
\((9, 0, 1)\) |
| ⑦再び桶から7升枡に油を移します。 | \((2, 7, 1)\) |
| ⑧7升枡から3升枡に油を移します。このとき、3升枡に 油がすでに1升入っているので、油は2升入ります。 |
\((2, 5, 3)\) |
| ⑨3升枡から桶に油を移すと、桶と7升枡に油を5升ずつ 分けることができました。 |
\((5, 5, 0)\) |
おまけ
ここで、油分け算のルールからはちょっと外れて、別な視点で話をします。
7升枡と3升枡が、ともに“直方体”の容器だったとします。すると、次のような工夫をすれば5升ずつに分けられます。
★水面が頂点を通る長方形になるように傾けて入れると、容量の2分の1の量が入る。
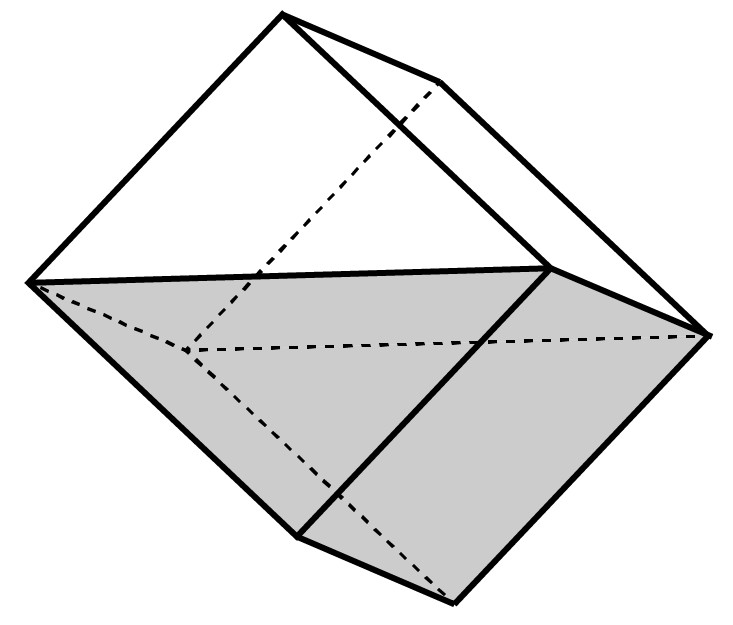
\(7升÷2=3.5升\)
\(3升÷2=1.5升\)
これらを合わせれば、\(3.5升+1.5升=5升\)
さらに、このような直方体の枡の使い方もあります。
(覚えておくと、いつか役に立つ機会があるかもしれません……。)
★水面が頂点を通る三角形になるように傾けて入れると、容量の6分の1の量が入る。
(三角すいの形に水が入る。これは、上の容量の2分の1入る入れ方の、さらに3分の1の量になる。)
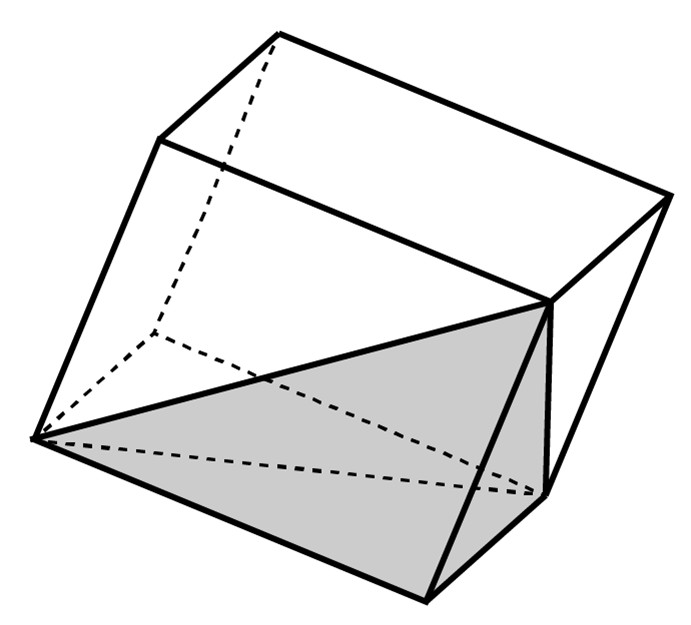
もっと考えてみよう!
つるかめ算と旅人算は、和算を使って解くことも、方程式を使って解くこともできました。 盗人隠しや油分け算の問題は、西洋数学で解こうとすると、多元連立線形方程式や不定方程式といわれる大学や高校で習う数学を使わなければなりません。しかし、和算を使えば、上記のように解くことができます。
江戸時代には、和算の問題を解いたり作ったりすることが、趣味や娯楽のひとつと考えられていました。実際に、多くの問題集が出版され、また自分が作った問題を神社に奉納した「算額」という絵馬も数多く残っています。
本記事をお読みいただいたことを機会に、たまには、このような和算の問題を解いてみたり、西洋数学の問題を和算を使って考えてみたりして、日本独自の算術の世界を楽しんでいただけたらと思います。
【関連記事】この記事では、和算について詳しく紹介しました。以下の記事でも数学の授業導入に活かせる題材を紹介しているので参考にしてみましょう。
・算数・数学の世界 「円周率の話」
・算数・数学の世界 「素数の話」
・算数・数学の世界 「小町算ってなんだ?」
これからの教育を担う若い先生たちに向けた、
学び・教育に関する助言・ヒント(tips)となるような情報を発信します。
何気なく口にする駄菓子(chips)のように、
気軽に毎日読んでもらいたいメディアを目指しています。